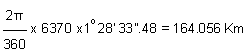Ex25-1 Find the shortest distance between a station (29° 52' N, 77° 54' E) at Roorkee and to a station (28° 34' N, 77° 06' E) at Delhi. Determine the azimuth of the line along which the direction of the shortest distance to be set out starting from Roorkee.
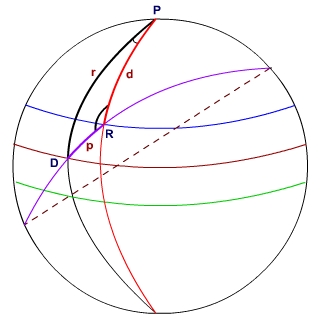
Figure Example 25-1
Solution :
The shortest distance between two stations on the surface of the earth lies along the circumfrence of the great circle passing through the stations.
Refering Figure Example 25-1, let us consider a great arc RD passing through the Roorkee and Delhi respectively. Thus, arc RD is the shortest distance between the stations. Let P be the pole of the earth. and PD and PR are arcs of meredians passing through Delhi and Roorkee stations respectively.
Then, PDR is a astronomical triangle, where
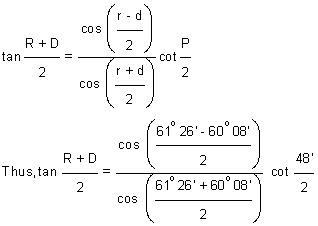
P = 77° 54' - 77° 06' = 48'
Distance PD, r = 90° - 28° 34' = 61° 26
Distance PR, d = 90° - 29° 52' = 60° 08'
Using equation (25A.3a),
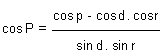
Or, cos p = cos d . cos r + cos P . sin d . sin r
= cos 60° 08' . cos 61° 26' + cos 48' . sin 60° 08' . sin 61° 26'
= 0.23826 + 0.76154 = 0.99966837
Therefore p = 1° 28' 33".48
Assuming, rdius of the earth, R = 6370 km.
Arc distance, RD =
For the determination of the direction from R to D, the angle R of the spherical triangle is required to be determined.
Using equation 25A.11a,
Therefore R + D = 179° 36' 34".12 ------------------------Equation 1
Again, using equation 25A.11b
= 3° 43' 24".07
Or, R - D = 123° 31' 05".20 ------------------------Equation 2
Solving Equation 1 & 2,
R = 151° 33' 49".66
Thus, the azimuth of the line to be set out at station R to proceed along shortest path to the station at Delhi is = 360° - R = 208° 26' 10".34