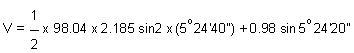Ex23-1 In order to carry out tacheometric surveying, following observations were taken through a tacheometer set up at station P at a height 1.235m.
Staff held Vertical at |
Horizontal distance from P (m) |
Staff Reading (m) |
Angle of Elevation |
Q
|
100 |
1.01 |
0° |
R
|
200 |
2.03 |
0° |
S
|
? |
3.465, 2.275, 1.280 |
5° 24' 40" |
Compute the horizontal distance of S from P and reduced level of station at S if R.L. of station P is 262.575m
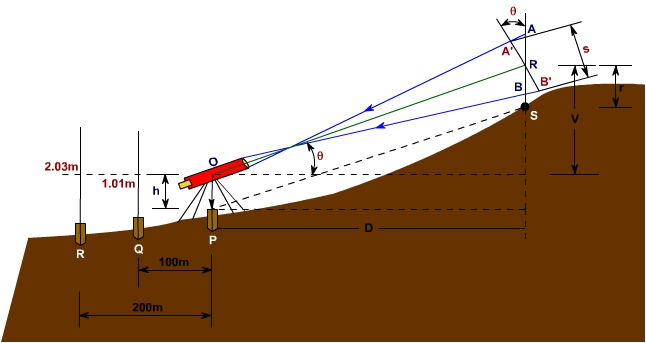
Figure Ex23-1
Solution :
Since the staff station P and Q are at known distances and observations are taken at horizontal line of sight, from equation 23.2
i.e. from D = K.s + C, we get
100 = K. 1.01 + C --------------- Equation 1
200 = K. 2.03 + C --------------- Equation 2
where K and C are the stadia interval factor and stadia constant of the instrument.
Therefore Solving equation 1 and 2 , 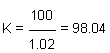
Substituting, value of K in Equation 1, we get
C = 100 - 1.01 x 98.04 = 0.98
Now, for the observation at staff station S, the staff intercept
s = 3.465 - 1.280 = 2.185 m;
Given, the angle of elevation (of a observation at S), q = 5° 24' 40"
Using equation 23.3 i.e., D = K s cos2 q + C.cos q, the horizontal distance of S from P is
D = 98.04 x 2.185 x cos2 5° 24' 40" + 0.98 cos 5° 24' 40"
= 212.312 + 0.9756 = 213.288 m
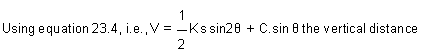
= (20.11 + 0.0924)m = 20.203 m
Thus R.L. of station S = R.L. of P + h + V - r
= 262.575 + 1.235 + 20.203 - 2.275
= 281.738 m