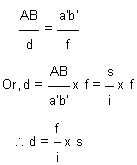(Figure 23.1) A tacheometer is temporarily adjusted on the station P with horizontal line of sight. Let a and b be the lower and the upper stadia hairs of the instrument and their actual vertical separation be designated as i. Let f be the focal length of the objective lens of the tacheometer and c be horizontal distance between the optical centre of the objective lens and the vertical axis of the instrument. Let the objective lens is focused to a staff held vertically at Q, say at horizontal distance D from the instrument station.
By the laws of optics, the images of readings at A and B of the staff will appear along the stadia hairs at a and b respectively. Let the staff interval i.e., the difference between the readings at A and B be designated by s. Similar triangle between the object and image will form with vertex at the focus of the objective lens (F). Let the horizontal distance of the staff from F be d. Then, from the similar Ds ABF and a' b' F,
as a' b' = ab = i. The ratio (f / i) is a constant for a particular instrument and is known as stadia interval factor, also instrument constant. It is denoted by K and thus
d = K.s --------------------- Equation (23.1)
The horizontal distance (D) between the center of the instrument and the station point (Q) at which the staff is held is d + f + c. If C is substituted for (f + c), then the horizontal distance D from the center of the instrument to the staff is given by the equation
D = Ks + C ---------------------- Equation (23.2)
The distance C is called the stadia constant. Equation (23.2) is known as the stadia equation for a line of sight perpendicular to the staff intercept.