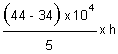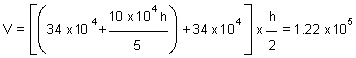Ex.18-1 In a hydro-electric project, the reservoir provides a storage of 5.9 million cubic meter between the lowest draw down and the top water level. The areas contained within the stated contours and the upstream face of the dam are as follows :
Contour (m) |
200 |
195 |
190 |
185 |
180 |
175 |
170 |
165 |
Area (104 sq m) |
44 |
34 |
28 |
23 |
20 |
16 |
11 |
8 |
If the R.L. of the lowest draw down is 167 m, find the reduced level of water at the full storage capacity of the reservoir.
Solution :
The area contained in lowest draw down level i.e. at 167 m is as follows :
Given, contour interval = 5 m
The area contained between 165 m and 170 m level is (11 - 8) x 104 = 3 x 104 sq m
i.e., For a height of 5 m, difference in area = 3 x 104 sq m
Therefore between 165 m and 167 m, i.e. for a height drift of 2 m, the area difference
= 1.2 x 104 sq m
The area contained in 167 m contour = (8 + 1.2 ) x 104 sq m = 9.2x 104 sq m
Now from given and calculated data and using trapezoidal rule
Contour |
Area contained (104) |
Volume contained between (104) |
Volume contained by (104) |
167 |
9.2 |
||
30.3 |
|||
170 |
11.0 |
30.3
|
|
67.5 |
|||
175 |
16.0 |
97.8 |
|
90.0 |
|||
180 |
20.0 |
187.8 |
|
107.5 |
|||
185 |
23.0 |
295.3 |
|
127.5 |
|||
190 |
28.0 |
422.8 |
|
155.0 |
|||
195 |
34.0 |
577.8 |
|
195.0 |
|||
200 |
44.0 |
772.8 |
So, at full storage capacity, the height of water level lies between 195 m and 200 m.
The volume of water beyond 195 m height is
(5.9 x 106 - 5.778 x 106) = 1.22 x 105 cu.m
Let h be the height of water level above 195 m height. Then area contained in (195 + h) m contour is
= 34 x 104 +
The volume between 195 m and (195 + h) m contour is
or, h2 + 34 h -12.2 = 0
Solving, we get h = 0.355 m
Thus the reduced level of water at the full reservoir capacity is (195 + 0.355) = 195.355 m