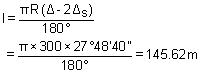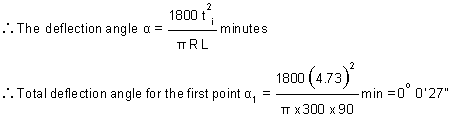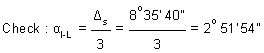Ex39-2 : Two tangent AB and BC intersect at chainage 1000 m the deflection angle being 45°. It is proposed to insert a circular curve of 300m radius with a transition curve 90m long at each end. Make all calculation necessary for setting out the curve by the method of deflection angle using peg interval as 15m on the transition curve and 30m on the circular curve.

Solution : Refer Figure 39.2, Given, deflection angle D = 45°

Radius of the circular curve, R = 300m

Length of the transition curve, L = 90m

(i) Shifts,

(ii) Total tangent length of the combined curve

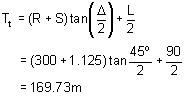
(iii) Spiral angle,

(iv)

(v) Length of the circular curve,

(vi) Chainages at

C' = chainage of C + l

= 920.27 + 145.62 = 1065.89m

T' = chainage of C'+ L

= 1065.89 + 90 = 1155.89m

Check :

Chainage of T' - Chainage of T = l + 2L

Or, 1155.89 – 830.27 = 145.62 + 2 x 90

Or, 325.62m = 325.62m (OK)

(vii) deflection angle for the first transition curve:

Chainage of T = 830.27m

Let the chainage of the first peg on the transition curve = 835.0m

Then, length of the first sub-chord of transition curve = 835.0 – 830.27 = 4.73m

Assume, normal chord length for transition curve, t = 15m;

Then, length of the last sub-chord = 90 – (5 x 15 + 4.73) = 10.27m

length of the first point , t₁ = 4.73m

length of the second point , t₂ = 15 + 4.73 = 19.73m

length of the third point , t₃ = 19.73 + 15 = 34.73m

t₄ = 49.73m, t₅ = 64.73m, t₆ = 79.73m, t₇ = 90m; (Check)

Similarly,

a₂ = 0° 8' 16", a₃ = 0° 25' 36", a₄ = 0° 52' 29"

a₅ = 1° 28' 55", a₆ = 2° 14' 54", a₇ = 2° 51' 54"

(viii) Deflection angle for the circular curve:

Length of circular curve, l = 145.62m

Let length of normal chord = 30m

Number of normal chord = 4

And length of sub-chord = 25.62m

Deflection angle,

<< Back | Next >>