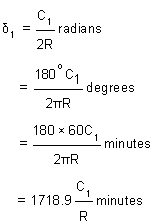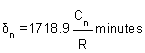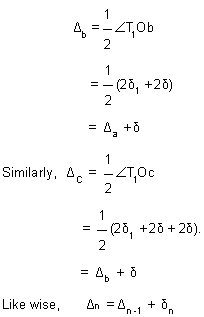In this method, curves are staked out by use of deflection angles turned at the point of curvature from the tangent to points along the curve. The curve is set out by driving pegs at regular interval equal to the length of the normal chord. Usually, the sub-chords are provided at the beginning and end of the curve to adjust the actual length of the curve. The method is based on the assumption that there is no difference between length of the arcs and their corresponding chords of normal length or less. The underlying principle of this method is that the deflection angle to any point on the circular curve is measured by the one-half the angle subtended at the centre of the circle by the arc from the P.C. to that point. [Rule 1 under "Fundamentals of geometry of Circular Curve" stated in lesson 37].

Let points a, b, c, d, e are to be identified in the field to layout a curve between T₁ and T₂ to change direction from the straight alignment AV to VB as in Figure 38.1(a). To decide about the points, chords ab, bc, cd, de are being considered having nominal length of 30m. To adjust the actual length of the curve two sub-chords have been provided one at the beginning, T₁ a and other, eT₂ at the end of the curve. The amount of deflection angles that are to be set from the tangent line at the P.C. are computed before setting out the points. The steps for computations are as follows:

Referring to Figure 38.1(b), let the tangential angles for points a, b, c,… be d₁, d,…, d, d_n and their deflection angles (from the tangent at P.C.) be D_a, D_b, ….. , D_n.

Now, for the first tangential angle d₁, from the property of a circle

Arc T₁ a = R x 2d₁ radians

Assuming the length of the arc is same as that of its chord, if C₁ is the length of the first chord i.e., chord T₁ a, then

(Note: the units of measurement of chord and that of the radius of the curve should be same).

Similarly, tangential angles for chords of nominal length, say C,

And for last chord of length, say C_n

The deflection angles for the different points a, b, c, etc. can be obtained from the tangential angles. For the first point a, the deflection angle D_a is equal to the tangential angle of the chord to this point i.e., d₁. Thus,

D_a = d₁.

The deflection angle to the next point i.e., b is D_b for which the chord length is T₁ b. Thus, the deflection angle

Thus, the deflection angle for any point on the curve is the deflection angle upto previous point plus the tangential angle at the previous point.

<< Back | Next >>