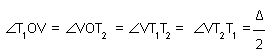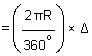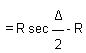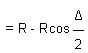Let T₁GT₂ be the circular curve that has been provided between the tangents AV and VC. The deflection angle, D between the tangents is measured in the field. The radius of curvature is the design value as per requirement of the route operation and field topography. The line joining O and V bisects the internal angles at V and at O, the chord T₁T₂ and arc T₁GT₂ . It is perpendicular to the chord T₁T₂ at F. From the Figure 37.1, RT₁ O T₂ = D and

To compute the elements of a circular curve, consider the radius of the curve OT₁ = OT₂ = R. Further, it is known that the RVT₁ O = RVT₂ O = 90° (since the tangent to a circle is perpendicular to the radius at the point of tangency). The elements of a circular curve required to lay it out in the field with reference to Figure 37.1 are as follows :

Length of Curve,

l = T₁ GT₂

--------------Equation (37.1)

Tangent Length,

T = length T₁ V = length T₂ V

--------------Equation (37.2)

Chainages of tangent point : The chainage of the point of intersection (V) is generally known. Thus,

Chainageof T₁ = Chainage of V - tangent length (T) --------------Equation (37.3)

Chainage of T₂ = Chainage of T₁ + length of curve (l) --------------Equation (37.4)

Length of the long chord (L) : Length of the long chord,

L = length T₁ FT₂

--------------Equation (37.5)

External distance (E) :

E = length VG

= VO - GO

--------------Equation (37.6)

Mid-ordinate (M) :

M = length GF = OG-OF

--------------Equation (37.7)

<< Back | Next >>