


: この文書について...
: Transportation Demand Analysis
: Collection of Transportation Demand
- Given the following data set, develop a trip table with four categories
of households. List the problems you face while doing so.
| Household |
Monthly |
Occupants |
Trips |
| number |
income |
between 6 |
produced |
| |
(1000 Rs.) |
and 60 yrs. |
per day |
| 1 |
10 |
2 |
4 |
| 2 |
15 |
5 |
4 |
| 3 |
35 |
5 |
14 |
| 4 |
30 |
6 |
14 |
| 5 |
40 |
3 |
8 |
| 6 |
15 |
5 |
6 |
| 7 |
20 |
3 |
3 |
| 8 |
32 |
3 |
8 |
| 9 |
40 |
3 |
9 |
| 10 |
38 |
2 |
6 |
| 11 |
40 |
6 |
10 |
| 12 |
12 |
6 |
6 |
| 13 |
35 |
2 |
8 |
| 14 |
40 |
2 |
7 |
| 15 |
15 |
2 |
3 |
- Using the trip table obtained in Problem 1, determine the total number
of trips produced from a zone with 2000 households in each category.
- Determine which of the following three trip distribution tables (giving
the trips made from Zone A to Zones B, C, and D) is likely to be obtained if
one used the maximum entropy model of trip distribution.
| |
B |
C |
D |
|
|
B |
C |
D |
|
|
B |
C |
D |
| A |
3 |
4 |
5 |
|
A |
4 |
4 |
4 |
|
A |
4 |
6 |
2 |
- For the 1000 shopping trips from Zone A, four destinations exist. The
destinations are Zones W, X, Y, and Z. The shopping areas available in
each of the zones and their distances from Zone A are given in the following
table. Assuming a proportionality constant of 0.35 and
assuming a thousand square meter of shopping area as one opportunity determine
the trip distribution from Zone A.
| Zone |
Shopping area |
Distance from Zone A |
| |
(in '000 sq.m.) |
(in km) |
| W |
2.0 |
5.0 |
| X |
1.0 |
8.0 |
| Y |
5.0 |
11.0 |
| Z |
3.0 |
5.0 |
- A Logit model is being developed for mode choice behaviour. The choice
is between two modes -- automobile and bus. The utilities derived from using
an automobile and a bus are,
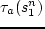 , and
, and 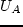 , respectively. The following
models for
, respectively. The following
models for 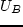 and
and 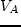 are proposed (note that, the notation used is,
are proposed (note that, the notation used is,
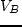 , where
, where 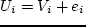 is a stochastic term):
is a stochastic term):
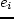 and
and 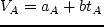 ; where,
; where, 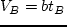 is the travel time by mode
is the travel time by mode 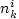 ;
; 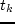 and
and 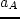 are
constants. Based on the above description, answer the following:
are
constants. Based on the above description, answer the following:
- Show that
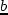 ; where
; where 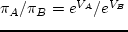 is the
probability of choosing Mode
is the
probability of choosing Mode  .
.
- What is the purpose of including a constant term in
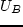 ?
?
- What sign should one expect for
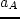 and why?
and why?
- If it is observed that people are more inclined to use their automobiles
(that is, they are biased towards the automobile mode) what sign should one
expect for
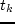 ?
?
- Suppose a new mode, say rail, is introduced and
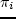 , what
changes can be observed in
, what
changes can be observed in 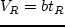 ,
, 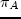 , and
, and 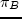 ?
?
- For the incremental assignment example problem given in the text assign
the O-D matrix in (a) three increments by dividing the matrix into three parts
in the ratio 40:30:30, and (b) in five increments by dividing the matrix into
five parts in the ratio 40:30:10:10:10. Compare the results and state what you
observe.
- Use user equilibrium method to assign the trips given in Problem 6.
- Show that for the example problem on user equilibrium given in the text
the objective function value at
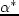 is 1975. Also show that the value of
is 1975. Also show that the value of
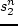 for
for 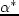 is 0.5964.
is 0.5964.



: この文書について...
: Transportation Demand Analysis
: Collection of Transportation Demand
root
平成17年10月17日
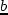 ; where
; where 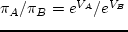 is the
probability of choosing Mode
is the
probability of choosing Mode 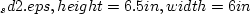 .
.
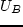 ?
?
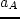 and why?
and why?
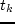 ?
?
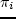 , what
changes can be observed in
, what
changes can be observed in 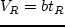 ,
, 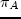 , and
, and 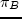 ?
?