The trip-generation models strive to predict the number of trips generated by a zone. These models try to mathematically describe the decision-to-travel phase of the sequential demand analysis procedure. It may be mentioned here that typically the term trip-generation is used to mean trip production -- generally the trips made from households --and trip attraction -- the trips made to a particular urban location or activity. However, it is felt that analysis of trip attractions should not be within the purview of trip-generation models which attempt to quantify a populations urge or propensity to travel. Rather, trip attractions are an outcome of the destination-choice phase of travel behaviour. Similar concerns about trip attractions being part of the trip generation phase of urban demand analysis have been also voiced in Kanafani [132]. In keeping with this, the present section discusses trip-generation primarily in the context of trip productions. Trip attractions are assumed to be an outcome of the destination-choice phase and are discussed in the section on trip- distribution models.
There are basically two different model structures for trip generation models -- the cross-classification models and the regression models. However, both these model structures incorporate the same basic factors which affect the trip generation of a zone; the models only differ in their characterization of these factors.
The factors (for any given trip purpose) which affect the trip generation of a zone are:
- The number of potential trip-makers in the zone; this data could be captured by variables like residential density, average household occupancy, age distribution of occupants, and so forth.
- The propensity of a potential trip-maker to make a trip; this is related to automobile ownership, accessibility to public transportation, and the like. For example, persons who own automobiles make more non-work trips than persons who do not own automobiles.
- Accessibility of the zone to potential destinations for a given trip-purpose satisfaction; variables like distance to potential destinations can capture this factor. For example, persons who live close to various recreational facilities may make more number of recreational trips than persons who live in areas which do not have nearby recreational facilities.
The cross-classification model, sometimes referred to as category-analysis model, is based on the assumption that the number of trips generated by similar households or households belonging to the same category is the same. According to this model if in Zone 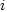 there are there are 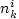 households in category households in category 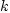 and if and if 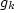 is the average rate of trip generation per household in category k then the relation of trips generated (or produced) by Zone i, Ti is given by is the average rate of trip generation per household in category k then the relation of trips generated (or produced) by Zone i, Ti is given by
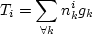 |
(1) |
The model predicts the trips produced by a zone by simply aggregating the total trips produced by all the households in that zone. However, two basic questions need to be answered here: (i) how do we define similar households, or alternatively how do we define categories of households, and (ii) how do we determine the rate of trip-generation for a given category of households. The answer to both these questions is: through empirical observations and analysis. What is done is that, first, data on demographic characteristics and trip -making behaviour of a large number of households are collected. This data is then analyzed to see what characteristics of the households are important in defining a homogeneous group -- the households which produce approximately the same number of trips.
Based on the above analysis, tables are made which define each category of households by listing its properties in terms of different demographic variables. For example, a particular category of households may be defined as households with 3 to 4 members in the age group 6 to 60, with income in the range of Rs. 30,000 to Rs. 40,000 per month, and one automobile. Finally, for each category of household the average number of trips generated are listed. The listing of the definition of categories and the associated trip -generation rates are generally referred to as trip tables.
This method of analysis although simple in its structure has few difficulties. The foremost is the problem with defining categories correctly -- at best it is very difficult. There are other problems like handling additional data on trip-generation behaviour -- the trip tables are not amenable to simple updating but generally have to be completely revamped every time new data is available.
In this model an additive functional form is assumed to exist between the factors which affect trip-generation and the number of trips generated. Generally, a linear function of the following form is used:
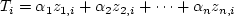 |
(2) |
where, 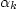 are parameters of the regression function and are parameters of the regression function and 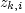 is the value of the is the value of the 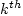 variable (such as income, automobile ownership, number of members in a household, and the like) for the i th zone. variable (such as income, automobile ownership, number of members in a household, and the like) for the i th zone.
As can be seen using this model to determine the number of trips generated by a zone is a simple matter when all the parameters of the regression function are known. Obviously, the parameters are determined by using some parameter estimation technique like Ordinary Least Squares or Maximum Likelihood Technique on empirically obtained data on 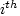 variables and variables and 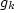 . For a good description of regression analysis and the parameter estimation techniques mentioned here, one may refer to any book on introductory statistical methods or basic econometrics; for example, Gujarati [95] and Wonnacot and Wonnacot [263]. . For a good description of regression analysis and the parameter estimation techniques mentioned here, one may refer to any book on introductory statistical methods or basic econometrics; for example, Gujarati [95] and Wonnacot and Wonnacot [263].
Discussion: Generally the models of trip-generation include variables which reflect the number of potential trip makers and the propensity of potential trip-makers to make a trip. However, none of the present models incorporate variables which reflect the accessibility factor. This is possibly the single largest factor as to why trip-generation models cannot very well predict the number of trips generated.
|