In this section the delay faced by vehicles at signalized intersections and the queues developed at signalized intersections are studied. Consider the plot shown in Figure 7. In this figure, the abscissa is time and the ordinate is the cumulative number of arrivals as well as the cumulative number of departures for a given stream (or approach) at an intersection. There are two lines in the figure. One shows a typical graph for cumulative number of arrivals on the given approach at a signalized intersection, the other shows the cumulative number of departures from the given approach at the signalized intersection. On the abscissa, the time is divided into slots named Cycle I, Cycle II, etc. These represent the cycles at the intersection. Each cycle is further subdivided into R and G. The R represents the duration of effective red (i.e., the time during which no vehicle on this particular approach crosses the intersection); similarly the G represents the duration of effective green (i.e., the time during which vehicles on this particular approach crosses the intersection).
The plot gives a reasonably complete picture of the arrival and departure
processes at the intersection. From such a plot one could obtain information
about both delay and queues. The horizontal distance at a value of ![]() on the
ordinate, for example, will give the delay faced by the
on the
ordinate, for example, will give the delay faced by the ![]() vehicle to
arrive at the intersection. Hence summing all such horizontal distances (or
equivalently the area between the two lines) will give the total delay faced
by all the vehicles arriving at the intersection. The total delay divided by
the total number of arrivals will provide the average delay.
vehicle to
arrive at the intersection. Hence summing all such horizontal distances (or
equivalently the area between the two lines) will give the total delay faced
by all the vehicles arriving at the intersection. The total delay divided by
the total number of arrivals will provide the average delay.
Similarly, the queues on the approach can be easily determined from the
figure. For example, the vertical distance between the two lines at time ![]() will give the queue length at the intersection approach at time
will give the queue length at the intersection approach at time ![]() . This
implies that the queue lengths at any given time can be obtained easily from
the figure and hence parameters like average queue length, variance of queue
lengths, etc. can also be obtained.
. This
implies that the queue lengths at any given time can be obtained easily from
the figure and hence parameters like average queue length, variance of queue
lengths, etc. can also be obtained.
However, obtaining such graphs for each and every intersection at all times is not feasible. Hence it is imperative that one analyzes the delay to vehicles and queues with an aim to derive equations which can give these quantities once data on arrival rates, cycle lengths, green times, red times, etc. are known. In the following, such a description of the analyses procedures is provided.
Delay analysis
To begin with assume that the arrival process is deterministic and vehicle arrive at a uniform rate. Further, assume that the system in unsaturated -- that is, the total number of vehicles that arrive in a period is less than the total number of vehicles that can be served by the system. These two assumptions mean that the arrival rate is such that all the vehicles that come in a cycle are cleared within the same cycle (like the situation in Cycle I of Figure 7).
The average delay to vehicles for this case then can be easily determined from
the figure shown in Figure 8. The figure shows a typical
cumulative arrival / departure graph against time for an unsaturated, uniform
arrival rate approach to an intersection. The slope of the cumulative arrival
line is ![]() , where
, where ![]() is the uniform arrival rate in vehicles per unit time.
The slope of the cumulative departure line is sometimes zero (when the light
is red) and sometimes
is the uniform arrival rate in vehicles per unit time.
The slope of the cumulative departure line is sometimes zero (when the light
is red) and sometimes ![]() (when the light is green); where
(when the light is green); where ![]() is the
saturation flow
rate obtained as the reciprocal of the saturation
headway explained earlier;
is the
saturation flow
rate obtained as the reciprocal of the saturation
headway explained earlier; ![]() is expressed as vehicles per hour of green per
lane or vphgpl.
is expressed as vehicles per hour of green per
lane or vphgpl.
From the figure (where ![]() is the duration of the cycle length and
is the duration of the cycle length and ![]() is the
duration of the effective green period) it can be seen that the total delay
(under the assumptions stated above),
is the
duration of the effective green period) it can be seen that the total delay
(under the assumptions stated above), ![]() , is given by
, is given by
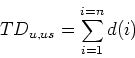 |
(6) |
Assuming that ![]() is large enough so that the discrete sum of
is large enough so that the discrete sum of ![]() is equal to the area of the triangle in the figure, the following can be
written:
is equal to the area of the triangle in the figure, the following can be
written:
| (7) |
From the figure, ![]() can be easily determined by noting that
can be easily determined by noting that
Determining ![]() from the above relation,
from the above relation, ![]() can be written as
can be written as
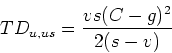 |
(8) |
From the above and noting that ![]() , the total number of vehicles
that arrived, is
, the total number of vehicles
that arrived, is ![]() the average delay under the above assumptions,
the average delay under the above assumptions,
![]() , can be obtained as:
, can be obtained as:
However, an approach to an intersection may not always stay unsaturated. There
may be periods of over-saturation during which the arrivals from one cycle
spill over to the next and so on. A similar situation can be seen in Cycle II
of Figure 7. Under this assumption, and the assumption that
arrival rate is still deterministic and uniform, the following plot of
cumulative arrivals / departures w.r.t. time
can be drawn (see Figure 8). In the figure it is assumed
that the arrival rate from 0 to time
T is ![]() , and that
, and that ![]() is large enough to cause over-saturation (i.e.,
is large enough to cause over-saturation (i.e., ![]() greater than,
greater than, ![]() , the maximum number of vehicles that can be served during
a cycle).
, the maximum number of vehicles that can be served during
a cycle).
From the figure it can be seen that the total delay under these assumptions,
![]() , is given by the sum of the area marked with horizontal stripes
(Area I) and the area marked with inclined stripes (Area II). This implies
that the average delay,
, is given by the sum of the area marked with horizontal stripes
(Area I) and the area marked with inclined stripes (Area II). This implies
that the average delay, ![]() , under these assumptions is the sum of the
average delay due to Area I and the average delay due to Area II.
, under these assumptions is the sum of the
average delay due to Area I and the average delay due to Area II.
The average delay due to Area II can be easily determined by assuming the
dashed line as the cumulative arrival line and using Equation 9.
However, first the slope of the dashed line needs to be determined and later
substituted for ![]() in Equation 9. If the slope of the dashed
line is taken as
in Equation 9. If the slope of the dashed
line is taken as ![]() (and noting that the slope of the inclined part of
the cumulative departure line is
(and noting that the slope of the inclined part of
the cumulative departure line is ![]() , the saturation flow rate) then
, the saturation flow rate) then
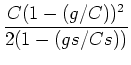 |
(10) | ||
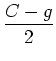 |
The average delay due to Area I can be determined by looking at the average
time between the cumulative arrival line and the dashed line. If the
horizontal distance (i.e., time in this case) between Point P and the dashed
line is taken as ![]() , then it can be said that the time between the cumulative
arrival line and the dashed line increases linearly from 0 to
, then it can be said that the time between the cumulative
arrival line and the dashed line increases linearly from 0 to ![]() over a time
period of 0 to
over a time
period of 0 to ![]() . From this it can be said that the average delay for
vehicles arriving between time 0 and
. From this it can be said that the average delay for
vehicles arriving between time 0 and ![]() is
is ![]() (Note that the area of the
triangle formed by the cumulative arrival line, a horizontal line from P and
the dashed line is given by
(Note that the area of the
triangle formed by the cumulative arrival line, a horizontal line from P and
the dashed line is given by ![]() , where
, where ![]() is the number of vehicles to
arrive till time
is the number of vehicles to
arrive till time ![]() ).
).
Similarly, the time between the cumulative arrival line and the dashed line
decreases linearly from ![]() to
to ![]() over a time period of
over a time period of ![]() to
to ![]() . Following
the same logic as above, the average delay due to Area I to vehicles arriving
between times
. Following
the same logic as above, the average delay due to Area I to vehicles arriving
between times ![]() and
and ![]() is
is ![]() . Hence, it can be said that the average
delay due to Area I is
. Hence, it can be said that the average
delay due to Area I is ![]() irrespective of when a vehicle arrives.
irrespective of when a vehicle arrives.
If one assumes the vertical distance of Point P from the dashed line as ![]() then
then
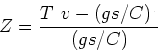 |
(11) |
Thus the average delay, ![]() is given as
is given as
In reality, however, more often than not the arrival is not deterministic, it is stochastic. Once it is assumed that the arrival is stochastic the above relations cannot be used and can at best function as approximate estimates. Assumption of stochastic arrivals leads us to analysis which is beyond the scope of this book. Hence, in this text, only the relations generally used to determine delay under the above assumptions are described.
One of the relations often used in determining delay is due to
Webster [#!web1!#]. Webster assumed that the arrivals are according to a
Poisson distribution, departures occur uniformly and at a maximum rate of ![]() ,
the average arrival rate
,
the average arrival rate ![]() is such that
is such that ![]() , and that the queueing
process runs under similar arrival and departure conditions long enough for
the system to stabilize to a steady state (where, for example, cycle to cycle
variations in average delay, average queue length, etc. are minimal). Based on
these assumptions and some simulation runs (where the arrival and departure
processes at a signalized intersection are simulated for various arrival
pattern and signal settings) Webster proposed the following expression for
average delay,
, and that the queueing
process runs under similar arrival and departure conditions long enough for
the system to stabilize to a steady state (where, for example, cycle to cycle
variations in average delay, average queue length, etc. are minimal). Based on
these assumptions and some simulation runs (where the arrival and departure
processes at a signalized intersection are simulated for various arrival
pattern and signal settings) Webster proposed the following expression for
average delay, ![]() :
:
The first term in the equation is the same as that given in Equation 9, the second term is the additional term which results from analyzing the process by assuming stochastic arrivals, the third term is a correction factor obtained from simulation studies. It is seen that this term is often between 5% to 15% of the sum of the first two terms. Hence the following simplified form of the above equation is sometimes used:
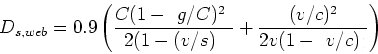
In practice, it is found that the ![]() estimates of delay are not good
for the entire range of
estimates of delay are not good
for the entire range of ![]() values. In general, when
values. In general, when ![]() values are close
to one (that is,
values are close
to one (that is, ![]() is close to
is close to ![]() ; this implies an increase in the
chances of over-saturation when the stochasticity in the
arrival rate causes the number of arrivals to be greater than
; this implies an increase in the
chances of over-saturation when the stochasticity in the
arrival rate causes the number of arrivals to be greater than ![]() ),
),
![]() overestimates the average delay. One
possible reason for this is that the derivation of the quantity assumes steady
state behaviour, which is never achieved at real intersections as
over-saturation by design occurs only in short spells. Other researchers
around
the world have developed other equations which are supposed to predict delays
more realistically. All of them predict values which are close to
overestimates the average delay. One
possible reason for this is that the derivation of the quantity assumes steady
state behaviour, which is never achieved at real intersections as
over-saturation by design occurs only in short spells. Other researchers
around
the world have developed other equations which are supposed to predict delays
more realistically. All of them predict values which are close to ![]() when
when ![]() is not high (say less than 0.8) while their estimates are much
lower when
is not high (say less than 0.8) while their estimates are much
lower when ![]() is high (say greater than 0.95). The 1985 Highway capacity
manual of USA [#!hcm1!#] proposes the use of one such expression for delay,
is high (say greater than 0.95). The 1985 Highway capacity
manual of USA [#!hcm1!#] proposes the use of one such expression for delay,
![]() , reproduced here as Equation 14. The expression
was
developed based on a large database on intersection delay.
, reproduced here as Equation 14. The expression
was
developed based on a large database on intersection delay.
The 1985 HCM [#!hcm1!#] cautions users against using this expression for
![]() . In
the 1998 HCM [#!hcm98!#] the calculation of delay has been further modified.
That
expression is not provided here as it uses many site specific empirical
constants which are not valid for Indian conditions.
. In
the 1998 HCM [#!hcm98!#] the calculation of delay has been further modified.
That
expression is not provided here as it uses many site specific empirical
constants which are not valid for Indian conditions.
Queue analysis
An involved discussion on analysis of queues at signalized intersections is not possible in this text as it requires substantial knowledge of stochastic queueing processes. However, certain characteristics of the arrival and departure processes from the point of view of queueing analysis are presented here so that the interested reader may pursue this topic further.
The primary purpose of doing a queueing analysis at a signalized intersection
is to be able to determine the probability distribution of queues that form.
That is, the aim should be to answer questions like, what is the probability
that there will be ![]() vehicles in a particular queue at any time. This is
important since not only values such as average queue length are important,
what is more important is an idea of the queue length distribution so that one
can determine lengths of auxiliary lanes 1 (see next
chapter for details) for pre-designated values of probability of overflow
(where the queue of vehicles is larger than the space provided by the
auxiliary lane) and probability of blockage (where the queue of vehicles on
the lane adjacent to the auxiliary lane is so large that it blocks the
entrance to the auxiliary lane).
vehicles in a particular queue at any time. This is
important since not only values such as average queue length are important,
what is more important is an idea of the queue length distribution so that one
can determine lengths of auxiliary lanes 1 (see next
chapter for details) for pre-designated values of probability of overflow
(where the queue of vehicles is larger than the space provided by the
auxiliary lane) and probability of blockage (where the queue of vehicles on
the lane adjacent to the auxiliary lane is so large that it blocks the
entrance to the auxiliary lane).
However, the theory of queues available so far are not able to model the queueing process at a signalized intersection in a simple manner. The primary reason for this is that the departure process is not a Poisson process. If one assumes (and correctly so) the time a vehicle waits at the top of the queue to be its service time, then it can be easily seen that the service time duration (to which the departure process is integrally connected) is not negative exponential. In fact the service time is either zero (if one reaches the top of the queue when the light is green) or it is equal to the duration of the red period (if one is the next to the last vehicle to have crossed the intersection); the probability of either of these service times being the service time of a particular vehicle is not easy to calculate. Matters can be further complicated if there is a permitted phase in the signal (as is sometimes the case for turning movements) where a vehicle can cross the intersection (during the non-green time) if a sufficient gap in the opposing stream exists.
Some researchers (see for example Kikuchi et al. [#!kik1!#]), however, have attempted to determine the probability distribution of queues through a Markov chain analysis of the queueing process. The interested reader may refer to Kikuchi et al.'s work cited above for a good understanding of the analysis procedure.
Example
On an approach to a signalized intersection, the effective green time is 30 seconds and the effective red time is 30 seconds. The arrival rate of vehicles on this approach is 360 vph between 0 and 120 seconds; 1800 vph between 120 and 240 seconds ; and 0 vph between 240 and 420 seconds. The saturation flow rate for this approach is 1440 vphgpl. The approach under consideration has one lane. Assume that at time = 0 seconds the light for the approach has just turned red.
Solution
The following parameter values are provided: ![]() s,
s, ![]() s,
s, ![]() vphgpl,
vphgpl, ![]() from 0 s to 120 s = 360 vph,
from 0 s to 120 s = 360 vph, ![]() from 120 s to 240 s =
1800 vph, and
from 120 s to 240 s =
1800 vph, and ![]() from 240 s to 420 s = 0 vph, and
from 240 s to 420 s = 0 vph, and ![]() , time for which there
exists a flow higher than
, time for which there
exists a flow higher than ![]() , is 120 s. Note,
, is 120 s. Note, ![]() vph.
vph.
Part 1
Figure 10 gives the required plot.
Part 2
Figure 11 gives the required plot.
Part 3
Between 0 second and 120 second the intersection is operating under
unsaturated conditions. Further, the arrival is deterministic and uniform.
Hence one could use Equation 9 to determine the average delay.
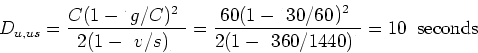
One could determine the average delay directly from the graph, by
noting that the area of either Triangle I or II in Figure 12
(which is the same as Figure 11 but with few extra
annotations) divided by the total number of arrivals during a cycle will give
the average delay.

Part 4
Between 120 seconds and 240 seconds the intersection is operating under over-saturated conditions. The arrival is deterministic and uniform. Hence one could use Equation 12 to determine the average delay.
One could also determine the average delay directly from the graph
(see Figure 12), by noting that,
Part 5
The average delay to all the vehicles between 0 and 240 seconds can
be obtained by dividing the total delay (faced by all vehicles) by the total
number of vehicles. Hence,
Of course one could find out the average delay here from the graph (the reader should do this).
Part 6
The arrival rate of vehicles from 0 to 120 seconds is 360 vph or 0.1
vps. Assuming that the fourth vehicle arrives before 120 seconds, the time of
arrival of the fourth vehicle is ![]() seconds. (Hence the assumption is
not violated).
seconds. (Hence the assumption is
not violated).
The departure rate of vehicles is ![]() vps. The time of
departure of the fourth vehicle, assuming that the fourth vehicle gets
discharged during the first green, is
vps. The time of
departure of the fourth vehicle, assuming that the fourth vehicle gets
discharged during the first green, is
![]() seconds. (Since
departure time is less than the start of the next red, the assumption is
valid).
seconds. (Since
departure time is less than the start of the next red, the assumption is
valid).
The delay to the fourth vehicle therefore is
The same observation can be made from the graph.
The delay to the sixtieth vehicle can also be read out from the graph (see Figure 12) as 144 seconds.
Part 7
As can be seen from the graph (see Figure 12) the maximum delay is 180 seconds.
Part 8
As can be seen from the graph (see Figure 12) the maximum queue length is 36 vehicles. At time = 240 seconds the queue length first becomes equal to 36 vehicles.
Part 9
As can be seen from the graph (see Figure 12) from
40 to 60 seconds and from 100 to 120 seconds there are no queues. For the rest
of the time there is a queue at the intersection. Hence, percentage of time
there is no queue at the intersection is
![]() . Hence
percentage of time there exists a queue is
. Hence
percentage of time there exists a queue is
![]() .
.
Part 10
One could determine the average queue length directly from the graph
(see
Figure 12), by noting that,