Delay and queue analysis

Unlike in the signalized intersection, the delay and queue analysis is taken up together here. From a queueing theory standpoint the flow on any of the approaches at an unsignalized intersection must be viewed as having the following characteristics:

• Various types of vehicles arrive at the intersection; these vehicles differ from one another in the time they spend at the stop line (henceforth referred to as service time). For vehicles which are at the top of the hierarchy, service time is nil and deterministic. For all the other types of vehicles the service time is stochastic and follow different distributions.
• The queue formed at the stop line has a ``first-in-first-out'' queue discipline. The queue may contain more than one type of vehicles depending on the number of lanes on the approach under consideration. For example, if there are separate turning and through lanes then queue will only contain turning vehicles as through vehicles do not queue. If, however, the approach has a lane which is shared by many types of vehicles then the queue has all the types of vehicles.

In analyzing any stochastic queueing system one needs to determine the arrival distribution and the service time distribution. In this case the arrival distribution may be assumed to be Poisson (if the intersection is away from any other source of interruption) or deterministic (if the intersection receives vehicles released by some other nearby signalized intersection) or a combination of the two. The service time distribution however needs to be determined given the modalities of the departure process.

The service time distribution will depend on the number of gaps that a vehicle rejects before accepting a gap and on the distribution of gaps themselves. As such the analysis is far beyond the scope of this book. The interested reader may refer to Drew [#!dre1!#] for a good development of this topic.

Even more complex is the analysis of the queue distribution and delay to vehicles. The complexity arises primarily due to the complex and different service time distributions of the various types of vehicles in the queue. Some idea of the process of analysis may be obtained from Chakroborty et al. [#!cha_us1!#].

Indian codes do not provide any expression which can be used to determine delay at unsignalized intersections under Indian traffic conditions. The 1998 HCM [#!hcm98!#] does provide relations to determine queue lengths and delay; but these are based on highly empirical considerations and are not provided here as Indian conditions at unsignalized intersections are quite different from those under which these equation were developed. Although, expressions are not available, in the following the factors on which queue length and delay at unsignalized intersections depend are described in the following. In this description the delay and queue of the movement being studied is referred to as 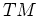$TM$.

Conflicting volume:

The volume of traffic in which the vehicles of TM look for gaps affect the queue length and delay. This is so, because, as the conflicting volume increases the number of adequate gaps decrease; this then increases the service times and hence the delay and the queue lengths.

Movement type:

Vehicles in movements which are lower in the hierarchy generally have to wait longer than vehicles of movements which are higher in the hierarchy. The reason for this is that often vehicles of low priority movements cannot accept an adequate gap because there is a vehicle of the higher priority also waiting and will use that gap. For example, consider a situation where there are two vehicles waiting; one belongs to the through movement from the minor stream (traveling North) while the other belongs to the right turning movement from the major (westbound) stream (a movement which is higher on the hierarchy than the former type of movement). Now a gap arrives in the eastbound major stream which could have been used by either of the vehicles; in such a situation the vehicle on the through movement from the minor stream will have to wait while the right turning vehicle uses the gap.

Critical gap:

As the critical gap increases the number of acceptable gaps in the conflicting movements reduce. This again increases the service times and hence the delay and the queue lengths.

Arrival rate:

As the arrival rate of vehicles in the TM increase the queue lengths increase and hence the delay also increases.

Speed:

It is seen that as speed of conflicting streams increase, the critical gap for drivers in the TM also increase. (This is possibly because, with increased speeds drivers want to be very sure before accepting gaps.). Increase in critical gaps have the effects described earlier.