Basic Concepts of Speed
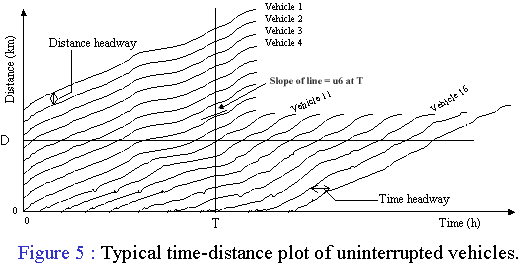
Typically speed of individual vehicles are measured at an instant or over a very short period of time. Such a speed is called Spot speed. If ui represents spot speed of vehicle i (say at time 't') then it is equal to the slope of the distance time line for the i th vehicle at time 't'. For example see the definition of u6 in Figure 5 (reproduced from Lecture 1).
In order to determine a representative speed for the entire stream typically the average speed of vehicles over a certain period of time (usually not more than 15 minutes) is determined. Two types of averages are typically determined;
Time Mean Speed
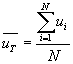
Space Mean Speed
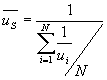
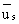 is a more appropriate measure of the stream conditions as it gives the average stream speed as the average of average speed of individual vehicles over a certain distance.
is a more appropriate measure of the stream conditions as it gives the average stream speed as the average of average speed of individual vehicles over a certain distance.
Advanced Concepts
As can be expected the speeds are not all the same; individual ui 's are actually distributed randomly around a certain average value. Various speed studies have been done and it has been seen that speed is distributed Normally (in order to learn more about Normal distribution click here) around the observed mean. Figure 6(a) shows a typical frequency distribution of speed on not-so-free-flowing expressway. The figure states that at this site 8 times out of 195 observations the speed was between 49.5 kmph and 50.5 kmph (this is plotted as a vertical line of height 8 on a x-axis value of 50 kmph- the mid point of the class 49.5-50.5)
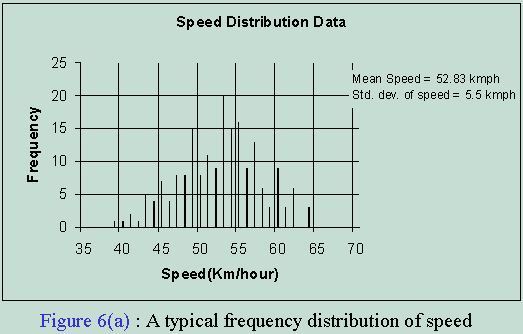
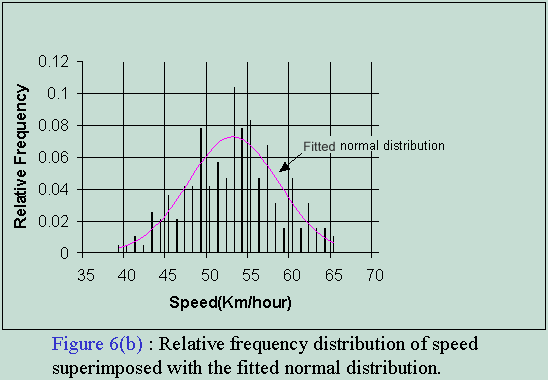
Figure 6(b) shows the same information as a relative frequency (drawn as vertical lines) versus speed plot. Relative frequency of a particular data is the frequency of that divided by the total number of observations. Also shown in the figure is a superimposed plot of a normal distribution fitted to the data. In this case it is meaningful to superimpose the density function on the relative frequency graphs i.e. Figure 6(b), as the class intervals are of unit length, like 48.5 to 49.5 kmph, 49.5 to 50.5 kmph, etc (Click here if you still don't understand). In order to fit the normal distribution the mean and standard deviation of the observed data are set equal to the mean and standard deviation of the theoretical distribution.
Studying speed distributions is important from various standpoints, like selection of design speed vis-a-vis speed limit, simulation of traffic streams , etc.
Basic Concepts of Density
Density is defined as the number of vehicles per unit length.It is measured at a given time over a specified distance. For example,as per the data given in Figure 5 the density at time T measured over a distance of D is 5/D vehicles per km. Note that 5 is the number of times the distance-time lines cross the vertical line at time = T. This indicates that at T there were 5 vehicles between 0 and D.
Density is also equal to the reciprocal of average distance headway.The distance heading is shown in Figure 5 (reproduced from lecture1) and indicates the distance between (similar points of) two consecutive vehicles.

Advanced Concepts
Density by definition is an average measure. It, as stated earlier, is related to the average distance headways. Individual distance headways however are all different and vary with time. A good and detailed description of distance headways will be provided in the discussion on Traffic Flow Theory.