When the soil sample has failed, the shear stress on the failure plane defines the shear strength of the soil. Thus, it is necessary to identify the failure plane. Is it the plane on which the maximum shear stress acts, or is it the plane where the ratio of shear stress to normal stress is the maximum?

For the present, it can be assumed that a failure plane exists and it is possible to apply principal stresses and measure them in the laboratory by conducting a triaxial test. Then, the Mohr circle of stress at failure for the sample can be drawn using the known values of the principal stresses.

If data from several tests, carried out on different samples upto failure is available, a series of Mohr circles can be plotted. It is convenient to show only the upper half of the Mohr circle. A line tangential to the Mohr circles can be drawn, and is called the Mohr-Coulomb failure envelope.

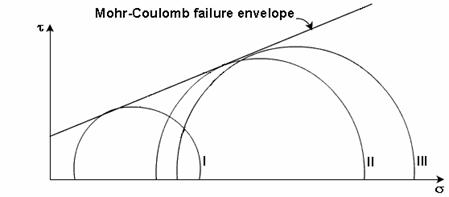
If the stress condition for any other soil sample is represented by a Mohr circle that lies below the failure envelope, every plane within the sample experiences a shear stress which is smaller than the shear strength of the sample. Thus, the point of tangency of the envelope to the Mohr circle at failure gives a clue to the determination of the inclination of the failure plane. The orientation of the failure plane can be finally determined by the pole method.

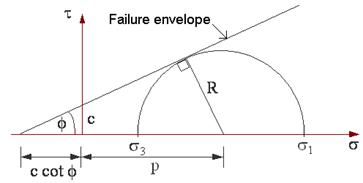
The Mohr-Coulomb failure criterion can be written as the equation for the line that represents the failure envelope. The general equation is

Where = shear stress on the failure plane
c = apparent cohesion
= normal stress on the failure plane
f = angle of internal friction

The failure criterion can be expressed in terms of the relationship between the principal stresses. From the geometry of the Mohr circle,

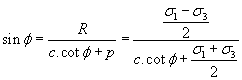
Rearranging,

where