Capitalized cost analysis:-

Capitalized cost represents the present worth of an alternative for a project that is going to serve for a longer period of time i.e. for an infinite period of time. As the name indicates, it refers to the present worth of mainly cost or expenditures (cash outflows) of the alternative over infinite period of time. Capitalized worth refers to present worth of expenditures and revenues of an alternative over infinite period of time.

The capitalized cost method is used for comparison of mutually exclusive alternatives which have perpetual service life (assumed to serve forever). The examples of this kind of projects are bridges, dams, irrigation projects, water supply systems for cities, pipeline projects etc. This method an also be used for finding out the capitalized cost of permanent fellowship/scholarship endowment in educational institutes and other organizations.

As already stated, capitalized cost/worth is the present worth of an alternative that has a perpetual or permanent cash flow series. The capitalized cost/worth of a perpetual cash flow having uniform amount series with end of year payments ‘A’ is obtained as follows.

The present worth of a uniform amount series is given by;

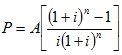
P = present worth, A = end of year payment of uniform amount series, i = interest rate per year and n = number of interest periods (already stated in Module 1)
The above equation can be rewritten as;

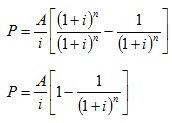
In the above expression, when ‘n’ approaches infinity (i.e. for perpetual cash flow series), the term “1/(1+i)n” gets neglected and present worth ‘P’ becomes capitalized cost/worth, the expression of which is given by;

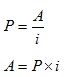
Thus the above expression can be explained by a simple example.
If a person deposits an amount of Rs.100000 in a bank at an interest rate of 10% per year, then how much money the person can withdraw from the bank every year without reducing the original deposit.

- The amount of interest accumulated (i.e. amount of money the person can withdraw without reducing the deposit) at the end of 1st year is Rs.10000 (100000 x 0.10).

- After withdrawal of Rs.10000 at the end of 1st year, the amount that will remain in his bank account is Rs.100000, which will again earn an interest amount of Rs.10000 at the end of 2nd year. After withdrawal of Rs.10000 at the end of 2nd year, the person will have again the same amount of Rs.100000 in his bank account that will further earn the same interest amount at the end of 3rd year. This process can be continued perpetually generating an interest amount of Rs.10000 (A = P x i) without changing the original deposit of Rs.100000. This example is similar to creating a scholarship endowment in a university that will give a scholarship of Rs.10000 every year indefinitely, by depositing Rs.100000 in a saving bank account at interest rate of 10% per year compounded annually.

The capitalized cost of a single amount occurring at regular intervals in future period of time is calculated by first finding out the equivalent uniform annual worth ‘A' of the uniform series and then dividing by the interest rate ‘i'.

The calculation of capitalized cost of an alternative is illustrated in the following example.

Example -17  

A public project has an initial cost of Rs.11000000 and annual operating and maintenance cost of Rs.700000. Further the project will have one time major repair work of Rs.2000000 at the end of 15 year. Find out the capitalized cost of the alternative if interest rate is 12% per year.

Solution:

The capitalized cost of the alternative is equal to sum of the initial cost, present worth of one time major repair cost and capitalized cost of the annual operating and maintenance cost.

The total capitalized cost of the alternative is given by;

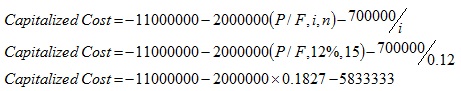
Capitalized cost = -Rs.17198733

Therefore the capitalized cost of the alternative for the public project is found to be Rs.17198733.