Table 2.3 shows a typical calculation. In the full mobilization case at top 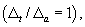 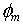 = = 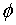 at the top and at the base at the top and at the base 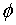 = 0 0. Considering this criteria, correction has been made using a correction factor of (35/36.3) at the top. Corrected values = 0 0. Considering this criteria, correction has been made using a correction factor of (35/36.3) at the top. Corrected values 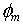 are shown in table 2.3. For other cases with are shown in table 2.3. For other cases with 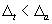 , the same maximum correction factor is applied at top to a linear variation of zero at the base. , the same maximum correction factor is applied at top to a linear variation of zero at the base.
The proposed equation as a lower bound to the points is given by, |