JKR Contact Mechanics Theory (contd...)
Here we'll find out how to obtain this actual contact radius
Consider the situation when no surface forces act, the contact radius is given as 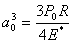 . The movement . The movement 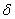 of the applied load is given by of the applied load is given by 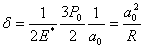
When attractive forces act between the surfaces the contact radius in equilibrium will be 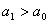 . Although, applied load remains at . Although, applied load remains at 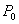 , an apparent Hertz load , an apparent Hertz load 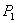 corresponding to the contact radius corresponding to the contact radius 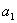 , defined as: , defined as:
Then the energy required to load the system of spheres to a contact radius 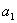 with a load with a load 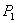 , in the absence of surface forces, can be calculated as: , in the absence of surface forces, can be calculated as:
Say, an intermediate load is 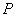 , and the corresponding contact radius is , and the corresponding contact radius is 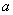 , then , then 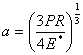 and the movement of the applied load is, and the movement of the applied load is,
The differential movement and the energy is
Hence the total energy stored in the spheres is
|