Herttzian Mechanics (contd...)
A similar expression can be written for the second surface:

The separation between the two surfaces is given as 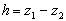 . .
We can now transpose equation 8.1 to a common set of axes 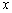 and and 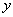 , ,
In which after suitable choice of axes, 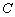 vanishes, leaving vanishes, leaving
Where 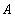 , , 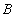 are constants and are constants and 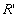 , , 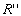 are principal relative radius of curvature. are principal relative radius of curvature.
If the axes of the principal curvature of each surface, i.e. the 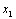 and and 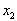 are inclined to each other by an angle are inclined to each other by an angle 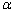 , then it can be shown that , then it can be shown that
and
|