Displacements specified in the loaded region:
So far in our discussion, we have specified the surface tractions as the boundary condition. But in most problems it is the displacements or a combination of displacement and traction that is specified.
We consider these problems by actually solving equation 4.26 which we rewrite as,
Thus we have a set of coupled integral equations for the unknown displacements 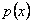 and and 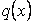 . .
However there is a singularity at 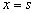 , which has been taken care of by different authors. We will not worry about their derivations, instead we will present only the end results. , which has been taken care of by different authors. We will not worry about their derivations, instead we will present only the end results.
Let's say the given boundary conditions are 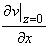 and and 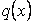 or or 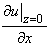 and and 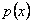 . Then it is easy to see that above equations get decoupled, taking general form . Then it is easy to see that above equations get decoupled, taking general form
where 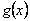 is a known function. T is a known function. T
he unknown component of traction 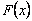 has a general solution of the form has a general solution of the form
If the origin is taken at the center of the loaded region then,
The constant 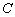 is determined by the total load, normal or tangential, from the relationship: is determined by the total load, normal or tangential, from the relationship:
|