Concentrated normal force (contd...)
Integrating the strain components, one can obtain the following solutions for the displacements.
If the points along the 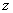 axis displaces only along the axis displaces only along the 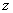 axis, then from the relation of axis, then from the relation of 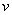 , , 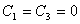 . .
At the surface, where 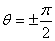 , ,
and
Where 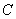 is a constant which can be obtained by choosing a point on the surface at a distance is a constant which can be obtained by choosing a point on the surface at a distance 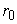 , where normal displacements is zero. Then we have. , where normal displacements is zero. Then we have.
Transforming the expressions for radial stress distributions into rectangular coordinates, we have
|