The significance of the persistence length (contd...)
Let us assume that the filament adopts only gentle curves with constant curvature and it does not close on itself, so that its shape can be uniquely parameterized by the angle 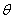 between the tangent vectors between the tangent vectors 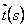 and and 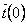 at the two ends of the filament. For an arc of a circle, at the two ends of the filament. For an arc of a circle, 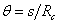 , so that the bending energy is expressed as: , so that the bending energy is expressed as:
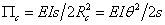 |
(34.2) |
The angle 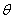 fluctuates back and forth and at higher temperature it has higher probability to attain larger amplitudes of oscillations. The magnitude of oscillations can be quantified by the mean value of fluctuates back and forth and at higher temperature it has higher probability to attain larger amplitudes of oscillations. The magnitude of oscillations can be quantified by the mean value of  i.e. i.e. 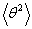 . For a filament with constant length, . For a filament with constant length, 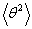 is the weighted average over three dimensional orientation of the filament position. This implies that one end of the filament defines the co-ordinate axis z and the other end describes the three dimensional position sampled by the polar angle is the weighted average over three dimensional orientation of the filament position. This implies that one end of the filament defines the co-ordinate axis z and the other end describes the three dimensional position sampled by the polar angle 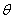 and azimuthal angle and azimuthal angle 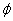 . Assuming that the shapes are all arcs of circles, the probability of each shape is equal to . Assuming that the shapes are all arcs of circles, the probability of each shape is equal to 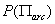 , so that , so that
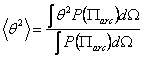 |
(34.3) |
The integration is carried out over the solid angle 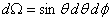 . The bending energy is independent of the azimuthal angle . The bending energy is independent of the azimuthal angle 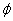 so that it can be integrated out, leaving so that it can be integrated out, leaving
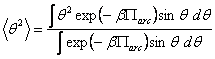 |
(34.4) |
Now let us assume that the filament is sufficiently stiff, so that energy increases very rapidly with increase in 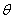 , in other word, the filament samples only small oscillations. Then the Boltzman parameter decays rapidly with , in other word, the filament samples only small oscillations. Then the Boltzman parameter decays rapidly with 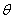 , implying that in equation 34.4 , implying that in equation 34.4 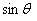 can be replaced by can be replaced by 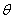 . .
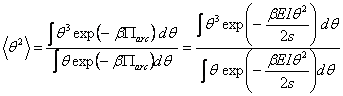 |
(34.5) |
Writing 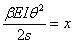 , equation 34.5 transforms to , equation 34.5 transforms to
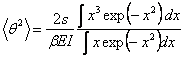 |
(34.6) |
In small vibrations, the upper limit can be extended to infinity so that both integrals yield 1/2. The expression for the mean square value of 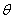 is then obtained as, is then obtained as,
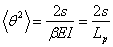 , , 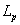 : persistence length : persistence length |
(34.4) |
|