Estimation of flexural rigidity of proteinaceous filaments like microtubules and Actin.

We know that due to thermal fluctuations soft filaments like microtubules and actin bends and constantly changes its shape. However, microtubule is much more rigid, so that the fluctuations due to thermal forces are too small for microtubules than that of actin. The thermal bending of the microtubule is characterized by representing its shape as summation of cosine functions of increasing frequency, that is by Fourier decomposing the profile of the rod. For example if we represent the profile of the filament in terms of tangent at every point s, (θ,s) then we can write:

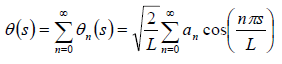(32.1)

where L is the length of the flexible rod and a_n is the amplitude of n^th Fourier mode. The cosine functions are chosen for computational convenience, but we could as well choose sine and cosine functions. Now due to thermal fluctuations, the shape of the rod changes, so that the amplitude of each mode also and they change independently of each other. For small bending, the bending energy per unit length of the filament is given by

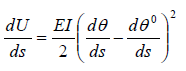(32.2)

Where θ₀ is the shape of the relaxed rod. Equation 32.2 on integration yields

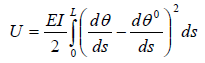(32.3)

Here, EI is the flexural rigidity of the rod and I is the moment of inertia defined as,

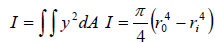(32.4)

Equation 32.2 and 32.3 emphasize the point that the concept of flexural rigidity developed so far for macroscopic filaments is also applicable for microscopic filaments despite their inherent complication in molecular structure.
Substituting the expression for θ(s) from equation 1 in equation 32.3, one obtains,

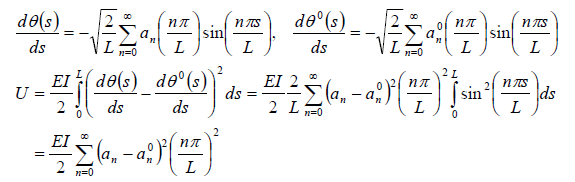(32.5)