| |
We have discussed earlier a similar problem in which an elastic slab of thickness 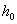 and length and length 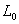 is subjected to compressive axial loads. Following this compression, the slab attains dimensions h and L respectively. Under plane strain approximations, the slab has been found to buckle at a critical compressive stress is subjected to compressive axial loads. Following this compression, the slab attains dimensions h and L respectively. Under plane strain approximations, the slab has been found to buckle at a critical compressive stress 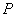 obtained from the solution of the characteristic equation: obtained from the solution of the characteristic equation:
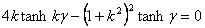 |
(31.1) |
where, 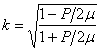 and and 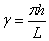 . For a cylinder, we replace h in the above expression by d. Solutions of equation 31.1 have been obtained for the asymptotic cases of . For a cylinder, we replace h in the above expression by d. Solutions of equation 31.1 have been obtained for the asymptotic cases of 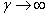 and and 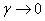 which have yielded the corresponding critical loads at which the buckling occurs. In the context of kinking phenomenon, however, the experiments clearly show that the axial length within which the zone of compressive stress remains concentrated, is which have yielded the corresponding critical loads at which the buckling occurs. In the context of kinking phenomenon, however, the experiments clearly show that the axial length within which the zone of compressive stress remains concentrated, is 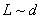 , so that , so that 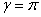 . Solution of equation 13.87 with this value of . Solution of equation 13.87 with this value of 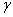 generates generates 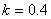 . Correspondingly the critical end load is found to be . Correspondingly the critical end load is found to be 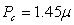 in terms of the shear modulus of the material of the gel. It can shown that at this value of the critical load, the curvature of the bent gel scales with the diameter as in terms of the shear modulus of the material of the gel. It can shown that at this value of the critical load, the curvature of the bent gel scales with the diameter as 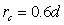 which is closed to the value observed in experiments. However a more rigorous analysis is needed in order to capture the kinking phenomenon. which is closed to the value observed in experiments. However a more rigorous analysis is needed in order to capture the kinking phenomenon.
|