Incompressible Elastic media:
Consider a unit cube with sides oriented along the 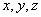 axes is subjected to normal stresses axes is subjected to normal stresses 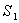 , , 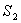 and and 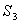 on its three faces, so that the cube turns into a parallelepiped with edges having lengths on its three faces, so that the cube turns into a parallelepiped with edges having lengths 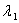 , , 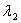 and and 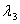 . These initial extension ratios represent the initial finite strain. These extension ratios must satisfy the following relation of incompressibility, . These initial extension ratios represent the initial finite strain. These extension ratios must satisfy the following relation of incompressibility,
In other word there are two independent strain variables for extensions along the co-ordinate axes. We then consider the strain energy as a function of a set of these two extension ratios:
The normal forces that act on the faces of the solid are 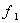 , , 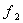 and and 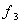 . Then the following law of conservation of energy should hold, . Then the following law of conservation of energy should hold,
Here, however, the three differentials are not independent but must satisfy the following relation of volume conservation,
Solving for 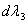 and substituting that in equation (28.5), we obtain and substituting that in equation (28.5), we obtain
Since 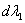 and and 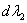 are independent, are independent,
or
|