| |
|
We can use the relation for 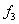 in equations (23.16) and (23.17), in equations (23.16) and (23.17), 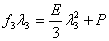 , which yields for (23.16) , which yields for (23.16)
Similarly, for equation (23.17), we obtain,
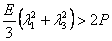 and and 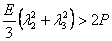 |
(23.19) |
These results then suggest that if 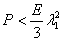 , , 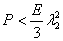 and and 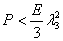 are satisfied then all three necessary and sufficient conditions as in equations (23.18) and (23.19) will be satisfied and the corresponding equilibrium state is stable. If are satisfied then all three necessary and sufficient conditions as in equations (23.18) and (23.19) will be satisfied and the corresponding equilibrium state is stable. If 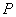 is negative, the equilibrium state is uniquely determined. is negative, the equilibrium state is uniquely determined.
|