| |
For the stretched sheet, 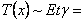 constant, while constant, while 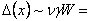 constant far from the clamped boundaries, so that constant far from the clamped boundaries, so that 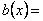 constant. At the clamped boundaries the boundary conditions are written as, constant. At the clamped boundaries the boundary conditions are written as,
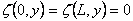 |
(18.7) |
Substituting in equation (18.7), a periodic solution of the form 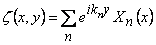 , where , where 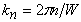 and and 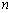 is the number of wrinkles, yields a Sturm-Liouville-like problem, is the number of wrinkles, yields a Sturm-Liouville-like problem,
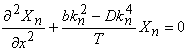 , , 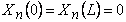 |
(18.8) |
Writing, 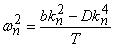 , equation 18.8 simplifies to , equation 18.8 simplifies to 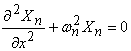 . We can use solutions of the form for . We can use solutions of the form for 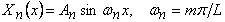 , Since the solution with least bending energy corresponds to , Since the solution with least bending energy corresponds to 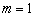 , so that , so that 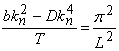 , rearranging, we have , rearranging, we have 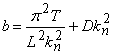 . Then the solution of . Then the solution of 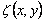 is written as, is written as, 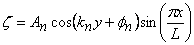 . Plugging this expression in 18.4, yields . Plugging this expression in 18.4, yields 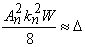 , relating the wave number and amplitude, so that we can write total energy as , relating the wave number and amplitude, so that we can write total energy as 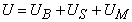 . Minimizing . Minimizing  , i.e. from , i.e. from 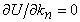 we obtain an expression for the wavelength: we obtain an expression for the wavelength:
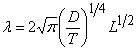 |
(18.9) |
Substituting this result in the condition of inextensibility along 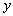 , ,
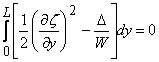 |
(18.10) |
We obtain an expression for the amplitude
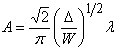 |
(18.11) |
Putting the expressions for flexural rigidity of the sheet, 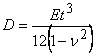 , tensile stress, , tensile stress, 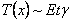 and transverse displacement, and transverse displacement, 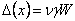 and substituting these expressions in equation 18.9, we obtain and substituting these expressions in equation 18.9, we obtain 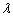 in terms of measurable quantities as, in terms of measurable quantities as,
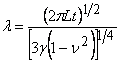 and and 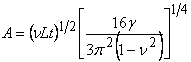 |
(18.12) |
The above expressions have been verified from experiments.
|