Let us now assume that bending occurs only in one dimension, so that 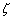 is a function of is a function of 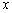 only and the above expression for the free energy simplifies to, only and the above expression for the free energy simplifies to,
 |
(16.6) |
If the bending of the plate is increased slightly so that 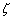 increases by increases by 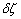 , then the differential amount of increase in free energy of plate is , then the differential amount of increase in free energy of plate is
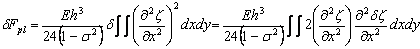 |
(16.7) |
Integration by parts of the above equation yields:
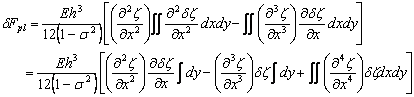 |
(16.8) |
If 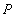 be the external force acting on the plate per unit area normal to the surface, then the work done by be the external force acting on the plate per unit area normal to the surface, then the work done by 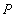 due to displacement due to displacement 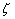 of the point of application of the force is of the point of application of the force is 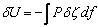 . .
Then it can be shown after some algebraic manipulation that the minimization of the total free energy of the system which includes the free energy of the plate and the work done by the external load results in the following equilibrium equation of a bent plate:
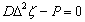 |
(16.9) |
where 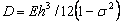 is the flexural rigidity of the plate. The boundary condition for solving this equation is different depending on whether the plate is clamped or supported. is the flexural rigidity of the plate. The boundary condition for solving this equation is different depending on whether the plate is clamped or supported.
(a) For plate whose edge is clamped, the boundary conditions are 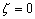 (no vertical displacement) and (no vertical displacement) and 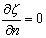 (the edge remains horizontal). The reaction force (the edge remains horizontal). The reaction force 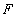 and the reaction moment and the reaction moment 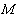 are written as are written as
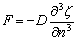 , , 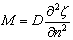 |
(16.10) |
(b) For a supported plate the moment of force becomes zero where it is supported, so that the following boundary conditions prevail: 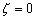 and and 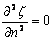 . .
|