Bending of thin plates
Here we will develop the general equation for bending of thin plates whose thickness is small compared with other two dimensions. When such a plate is bent, it is stretched in the convex part and compressed in the concave side. The stretching decreases as one penetrates into the plate till becoming zero at the neutral surface where there is no stretching or compression, at the other side of the neutral surface, the deformation changes sign.

Let us consider a co-ordinate system with origin on the neutral surface and the 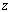 -axis normal to it. The -axis normal to it. The 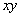 -plane is that of the un-deformed plate. Say, -plane is that of the un-deformed plate. Say, 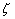 is the vertical displacement of a point on the neutral surface along the is the vertical displacement of a point on the neutral surface along the 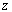 coordinate. Here, we consider small bending of the plate so that coordinate. Here, we consider small bending of the plate so that 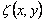 is small with respect to the thickness is small with respect to the thickness 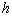 of the film. Other components of the displacement in the of the film. Other components of the displacement in the 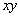 -plane are negligibly small relative to -plane are negligibly small relative to 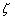 . Thus on the neutral surface the components of displacement vector are: . Thus on the neutral surface the components of displacement vector are: 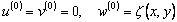 . .
|