Finally the expression for the dimensionless hydrostatic pressure 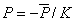 ( (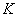 is the bulk modulus) is obtained as, is the bulk modulus) is obtained as,
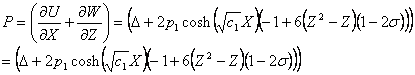 |
(11.20) |
Thus the expression for pressure is a function of 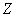 . However, let's say we are considering a nearly incompressible material, so that at . However, let's say we are considering a nearly incompressible material, so that at 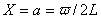 , , 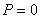 , ,
Then,
By substituting the above expression in 7.20, we obtain
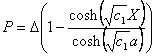 |
(11.21) |
Now we integrate equation 7.21 to obtain the dimensionless compressive force,
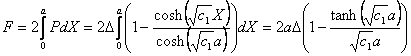 |
(11.22) |
Expanding 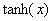 in series, we have in series, we have
So that, equation 7.22 turns to
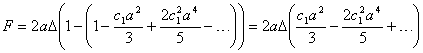 |
(11.23) |
Considering only the first term in the above equation and noting that the dimensionless load is given as, 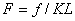 , we obtain an expression for force on as, , we obtain an expression for force on as,
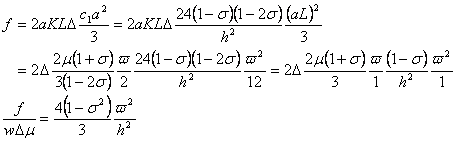 |
(11.24) |
Hence for an incompressible material, 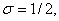 so that, so that, 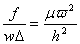
At 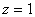 , ,
|