Contact of two cylinders with their axes parallel to the y-coordinate:
Here, we first determine the gradient of displacement, which from equation (10.2) is obtained as
However, from equation 4.27, the gradient of displacement for a distributed normal load, in absence of shear load, can be written as,
Where 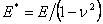 . Matching the right hand sides of the above two equations, we have, . Matching the right hand sides of the above two equations, we have,
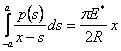 |
(10.7) |
Equation (10.7) has the following general form the solution of which has been worked out,
Here the constant 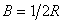 and the exponent of and the exponent of 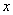 is is 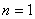 . The integration of equation10.8 obtained as, . The integration of equation10.8 obtained as,
Where 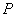 is the total load applied on per unit length of the contact area. The quantity is the total load applied on per unit length of the contact area. The quantity 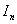 has the following form, has the following form,
|