Pure deformation and rigid body motion
Point to be noted here is that if the quantities 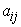 are given, the transformation of the coordinates of a point will not be completely defined, because, are given, the transformation of the coordinates of a point will not be completely defined, because, 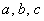 will still remain undetermined. But these quantities do not influence the deformations because they define only the rigid translation of the body. will still remain undetermined. But these quantities do not influence the deformations because they define only the rigid translation of the body.
Let us now define the quantities 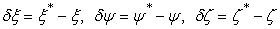 which are components of vector which are components of vector 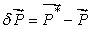 , or the displacement vector. Then , or the displacement vector. Then
We want to know the constraints on the tensor 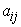 that will result in rigid body motion and no deformation. that will result in rigid body motion and no deformation.
Basically we want to find out the condition that the magnitude of the vector 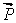 or the square of its modulus or the square of its modulus 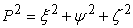 remains unaltered due to the transformation. Restricting ourselves to infinitesimal transformation, that is neglecting higher order terms, remains unaltered due to the transformation. Restricting ourselves to infinitesimal transformation, that is neglecting higher order terms,
In order that 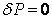 , it is imperative that , it is imperative that
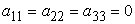 and |
| (1.10) |
which implies that 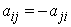 . Then equation 1.8 can be written as, . Then equation 1.8 can be written as,
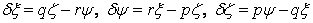 |
(1.11) |
where 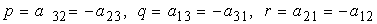 . These quantities are infinitesimal angles of rotation about the coordinate axes and are called the components of rotation. . These quantities are infinitesimal angles of rotation about the coordinate axes and are called the components of rotation.
|