This is the Young-Laplace equation for axisymmetric surfaces. It is a non-homogeneous second-order non-linear differential equation. This equation may have a unique solution, no solution or many solutions. A frequently used simplification is that for weakly curved surfaces,

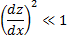
Some special cases

1. Homogeneous Young-Laplace equation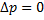

One possible solution (trivial solution) is a flat surface situation, i.e. 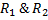both going to infinity. Another solution is a thin film formed between two loops kept at a distance away (Fig. 2.7).

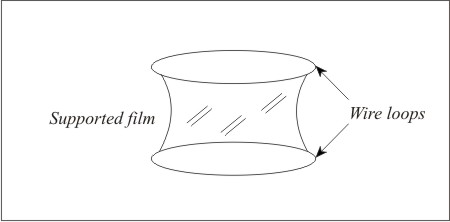
Figure 2.7. A thin film supported by two thin wire loops

2.

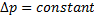
Then 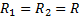. This means that the surface is spherical.