The plot has been shown in the figure below (Fig. 3.6).
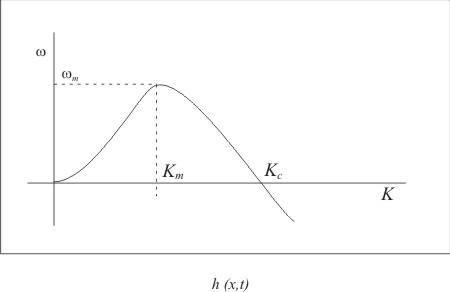
Figure 3.6. Growth coefficient versus wave number
Observations
For 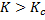 , ,  becomes negative. This qualitatively means that any perturbation with a very small wavelength would die down. becomes negative. This qualitatively means that any perturbation with a very small wavelength would die down.
Sources of disturbance could be mechanical perturbations or thermal perturbations. In the present case, all the modes corresponding to values of 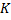 between 0 and between 0 and 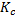 lead to instability. lead to instability.
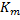 is called the dominant mode as it grows the fastest. is called the dominant mode as it grows the fastest.
In order to find 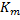 , we put , we put 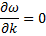
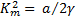
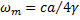
And to find 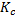 , we put , we put 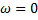 . .
Number of droplets arising due to instability 
If 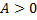 , the fluid partially wets the surface, which means the fluid layer breaks up into droplets. , the fluid partially wets the surface, which means the fluid layer breaks up into droplets.
This solution is valid only very close to equilibrium states.
Linear stability analysis is a powerful tool. It helps us analyze the stability of the system around an equilibrium state. But it has its limitations too. It does not give us information about the system over a long time scale. It only gives us the length scales of the deformation. For example, it does not tell us how long it would take before the film ruptures.
|