This linearization around h0, leads to the following expression,
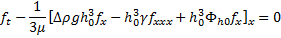 |
(3.11) |
Note that the above differential equation involves only even-ordered derivatives. Thus, it represents a stationary wave, and the solution to this equation is of the form
This solution is periodic in position and exponential in time.
One can verify this solution by substituting it back in the differential equation. This gives
The above relation is known as dispersion relation or characteristic equation or compatibility condition.
Here,
 is called the growth coefficient, and is called the growth coefficient, and
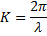 is called the wave number. is called the wave number.
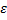 is the amplitude of the initial perturbation. is the amplitude of the initial perturbation.
If 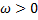 , the perturbation would grow. So, it causes instability. , the perturbation would grow. So, it causes instability.
If 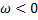 , the perturbation would decay. So, it would move towards stability. , the perturbation would decay. So, it would move towards stability.
If 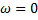 , it is the critical boundary between instability and stability. , it is the critical boundary between instability and stability.
|