Analysis of the solution

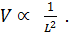1. This means that if the length is large, drainage would slow down. This is because of the viscous resistance.
2. As 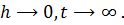This may lead us to believe that the two surfaces will not come together. But actually this isn’t true because when the surfaces are close together, Van-Der Waals forces will come into play and they will affect the system.

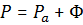
When the film thickness reduces to molecular scale, the intermolecular interactions become significant.

(3.6)

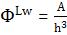
Substituting this in the differential equation

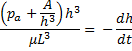
Now we can observe that as h becomes very small, velocity becomes constant. This implies that coalescence would occur in a finite time.

If the exponent of h is smaller it a leads to deceleration as the surfaces approach each other and contact occurs in infinite time. On the other hand, if the exponent of h is larger it results in acceleration and the two surfaces crash into each other.

Thus we can see that Lipshitz-van der Waals interactions lead to macroscopically verifiable interactions.