| |
So a system can be in a locally stable (meta-stable) or in a globally stable state. Given sufficient time, a system in a meta-stable state would escape to a globally stable state due to random perturbations.
The probability that a system will remain in a particular equilibrium state is governed by the Arrhenius factor, 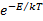 . Here, . Here, 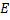 is the energy barrier and is the energy barrier and 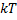 represents the thermal energy. represents the thermal energy.
In the example discussed above, the probability of the duster getting toppled and escaping to the globally stable state is proportional to 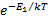 . Similarly, the probability that it gets flipped back to its original position is proportional to . Similarly, the probability that it gets flipped back to its original position is proportional to 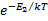 . Since . Since 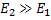 it is much more likely that the vertical duster will fall down to reach the horizontal state. It is quite obvious that it is highly unlikely that once the duster reaches the globally stable state it will flip back to the meta-stable state. This agrees with what we see in real life, since we quite often see a vertical duster falling down to a horizontal position, but never does a horizontal duster stand up vertically. (Although, in real life, the duster generally falls down due to external factors and not random perturbations.) it is much more likely that the vertical duster will fall down to reach the horizontal state. It is quite obvious that it is highly unlikely that once the duster reaches the globally stable state it will flip back to the meta-stable state. This agrees with what we see in real life, since we quite often see a vertical duster falling down to a horizontal position, but never does a horizontal duster stand up vertically. (Although, in real life, the duster generally falls down due to external factors and not random perturbations.)
Steady states
For a system, the states in which the system energy shows an extremum (maximum or minimum) are termed as steady states.
In case of open dissipative systems, we need the governing equations in order to study their stability, and the points of stability for such systems are generally referred to as steady states.
On the other hand, for closed systems the energy functions are usually available, and the points of stability for such systems are referred to as equilibrium states. Equilibrium cannot be attained in open systems. |