| |
| Lagrangian approach: |
| Identify (or label) a material of the fluid; track (or follow) it as it moves, and monitor change in its properties. The properties may be velocity, temperature, density, mass, or concentration, etc in the flow field. |
| Refer the above-figure. The ‘material’ or ‘particle’ of the fluid ‘A’ at time t has moved to some other location at time t’. Its property, say temperature, is recorded, as the material moves in the flow-field: |
 |
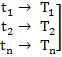| Note that the recorded temperatures are associated with the same fluid particle, but at different locations and at different times. |
| Think of a temperature sensor attached to a balloon, both having negligible mass and floating in the atmosphere and recording the atmosphere-temperature or the temperature of the flow-field. In such case, the following temperature-data are recorded by the sensor: |
|
 |
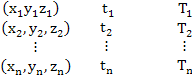The time change of the temperature in such a measurement is denoted as 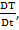 which is called material derivative or substantial derivative. It reflects time change in the temperature (or any other properties) of the labeled /marked/tagged fluid particles as observed by an observer moving with the fluid. Lagrangian approach is also called “particle based approach”. |
| |
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|
|
