It is important to note that the potential theory or inviscid flow–condition predicts ‘zero–drag’ on a solid surface. The common examples of potential flow are source/sink, free vortex, doublet, and Rankine’s half–body. We skip the analysis of such flows.   To overcome the paradox of zero drag on a solid surface, Prandtl (1903) came–up with the boundary–layer theory. As per the main postulate of the theory, the viscous term cannot be dropped from the NS equation for the high–Reynolds number flow. Physically, viscous effects are important at or near the solid surface, even at high Reynolds number.     By choosing the appropriate characteristic variables, it can be shown that one of the viscous terms, namely 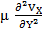  must be retained. This is possible if we assume that the characteristic length in y–direction is much smaller than that in the x–direction.