Module 8: Flow at low and high Reynolds numbers
  Lecture 26: Creeping flow, Stokes-law and terminal velocity
 
 
Low Reynolds-number Flow: Under this condition, the viscous effects dominate the inertial effects.
 

Mathematically  and

 Such flow is called as creeping-flow

One of the most common examples of creeping flow is the flow past a spherical object at low Reynolds number.

We will not derive the expression for velocity fields in this lecture. Readers can refer to an advanced book on fluid mechanics.

However, it may be mentioned that the total force comprising of normal and shear can be combined to obtain the well–known Stoke’s law for the drag (force acting along the flow–direction) on a sphere:
 

 

 

Where,  
             
             

   Fluid Viscosity
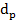= Diameter of the particle
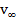=Relative velocity of the particle with respect to the fluid–velocity
 
This equation is valid for