| |
| In earlier lecture, we obtained an expression for pressure-drop in a pipe or tube for the flow of a fluid under laminar conditions: |
|
The expression was obtained analytically by applying the NS equation and integrating the same with appropriate boundary conditions. The expression (also known as the Hagen–Poiseuille equation) was also derived by making the force-balance over a CV in the tube. It is important to note that such mathematical treatment can be carried out, only if the flow is laminar.
|
- Laminar flow refers to the flow which can be characterized by streamlines. The flow is controlled by viscous effects and the fluid velocity is relatively smaller. A parabolic-velocity profile obtained in a tube for a fluid–flow at small velocity is a good example of laminar-flow conditions.
|
|
(Fig. 23a) |
Turbulent flow: Such flow occurs at relatively larger velocities and is characterized by chaotic behavior, irregular motion, large mixing, and eddies. For such flow, inertial effects are more pronounced than viscous effects. Mathematically, velocity field is represented as 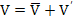 , or the velocity fluctuates at small time scales around a large time-averaged velocity. Similarly, , or the velocity fluctuates at small time scales around a large time-averaged velocity. Similarly, 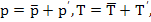 etc etc |
| |
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|
|