Methods for solving linear algebraic equations can be categorized as direct
and iterative schemes. There are several methods which directly solve equation
(5). Prominent among these are such as Cramer's
rule, Gaussian elimination and QR factorization. As indicated later, the
Cramer's rule is unsuitable for computer implementation and is not discussed
here. Among the direct methods, we only present the Gaussian elimination here
in detail.
3.1 Gaussian Elimination and LU Decomposition
The Gaussian elimination is arguably the most used method for solving a set of
linear algebraic equations. It makes use of the fact that a solution of a
special system of linear equations, namely the systems involving triangular
matrices, can be constructed very easily. For example, consider a system of
linear equation given by the following matrix equation 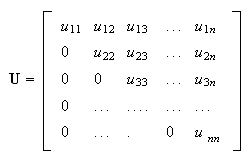 --------(16)Here, --------(16)Here,  is a upper triangular matrix such that all elements below the main diagonal
are zero and all the diagonal elements are non-zero, i.e. is a upper triangular matrix such that all elements below the main diagonal
are zero and all the diagonal elements are non-zero, i.e. 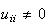 for all i. To solve the system for all i. To solve the system 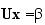 ,
one can start from the last equation ,
one can start from the last equation 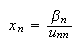 --------(17)and
then proceed as follows --------(17)and
then proceed as follows 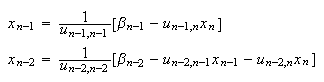 |