as 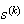 is assumed to be a descent direction. Thus, we take is assumed to be a descent direction. Thus, we take 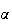 corresponding to corresponding to 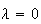 and try to find a point and try to find a point 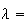 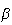 such that such that 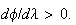 The point The point 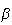 can be taken as the first value out of can be taken as the first value out of 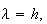 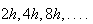 for which for which 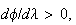 where where 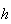 is some pre-assigned initial step size. As is some pre-assigned initial step size. As 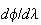 changes sign in the interval changes sign in the interval ![$[0,\beta ],$](../../../images/module4/graphics/Module_4_Solving_Ax=b__992.gif) the optimum the optimum 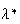 is bounded in the interval is bounded in the interval ![$[0,\beta ].$](../../../images/module4/graphics/Module_4_Solving_Ax=b__994.gif)
The next step is to approximate 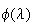 over interval over interval ![$[0,\beta ]$](../../../images/module4/graphics/Module_4_Solving_Ax=b__996.gif) by a cubic interpolating polynomial for the form by a cubic interpolating polynomial for the form |