From the knowledge of linear elastic behaviour of the orthotropic materials it is clear that the shear response is uncoupled from the normal response. Hence, in-plane shear modulus 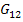 can be determined directly from a tensile test on a can be determined directly from a tensile test on a 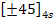 laminate. laminate.
Now the shear strain 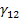 in principal material coordinates can be found by transformation of the measured axial and transverse strains in principal material coordinates can be found by transformation of the measured axial and transverse strains 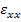 and and 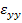 . It should be noted that the shear strain . It should be noted that the shear strain 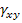 is zero for orthotropic laminates under tension and is zero for orthotropic laminates under tension and 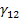 is independent of is independent of 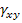 for for 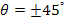 (see the strain transformation relations). Thus, from the strain transformation relations, we can get the shear strain in principal material directions as (see the strain transformation relations). Thus, from the strain transformation relations, we can get the shear strain in principal material directions as
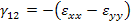 |
(8.17) |
Thus, from the definition of the shear modulus we get
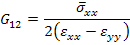 |
(8.18) |
The above equation can be rearranged in the following manner to express the shear modulus in terms of effective properties of 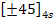 laminate. laminate.
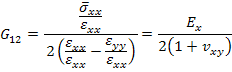 |
(8.19) |
Here, 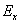 is the effective modulus of the is the effective modulus of the 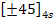 laminate. laminate. |