| |
For example, in case of 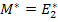 for a circular fibres in a square array, for a circular fibres in a square array, 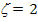 and for rectangular fibres cross section of length and for rectangular fibres cross section of length 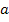 and width and width 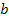 in a hexagonal array, in a hexagonal array, 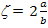 where where 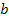 is in the direction of loading. Similarly, for is in the direction of loading. Similarly, for 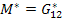 for circular fibres in a square array for circular fibres in a square array 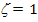 , and for rectangular cross-section with length , and for rectangular cross-section with length 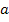 and width and width 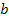 in a hexagonal array, in a hexagonal array, 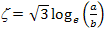 , where , where  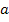 is in the loading direction. is in the loading direction.
Note: In case of transversely isotropic material in 23 plane, the constitutive relations are given as
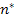  |
(7.296) |
and
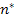  |
(7.297) |
Here, the moduli 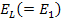 and and 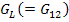 refer to the values in the longitudinal or axial direction of straining and refer to the values in the longitudinal or axial direction of straining and 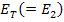 and and 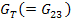 refer to the values in transverse plane. Further, the Poisson’s ratios are defined as refer to the values in transverse plane. Further, the Poisson’s ratios are defined as 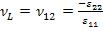 and and 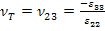 under the uniaxial tensions in 1 and 2 directions, respectively. under the uniaxial tensions in 1 and 2 directions, respectively.
|