| |
Halpin-Tsai Semi-Empirical Relations
A set of semi-empirical relations have been developed by Halpin and Tsai for easy design procedure. These relations were developed by curve fitting to the results that are based on elasticity. These relations are called semi-empirical relations because the parameters involved in these relations have some physical significance. In the following we give these relations.
The longitudinal Young’s modulus is same as given by rule of mixtures using strength of materials approach. Thus,
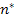 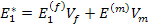 |
(7.288) |
Further, the axial Poisson’s ratio is the same as given by the rule of mixtures using strength of materials approach. Thus, the axial Poisson’s ratio is
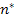 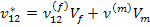 |
(7.289) |
The Hill’s Moduli are given as
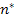 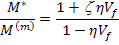 |
(7.290) |
where
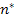 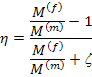 |
(7.291) |
Further, 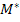 stands for stands for 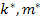 or or 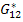 and and 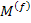 and and 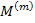 stands for corresponding values for fibre and matrix, respectively. Here, stands for corresponding values for fibre and matrix, respectively. Here, 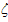 is a measure of reinforcement geometry which depends upon loading conditions and geometries of the inclusion, that is, fibre. is a measure of reinforcement geometry which depends upon loading conditions and geometries of the inclusion, that is, fibre.
The parameters used in the Equation (7.290) have physical significance. The limiting values give following significant information:
-
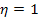 corresponds to a situation that the inclusions are rigid. corresponds to a situation that the inclusions are rigid.
-
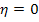 corresponds to a homogeneous material corresponds to a homogeneous material
-
And for voids , 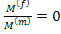 , then . , then .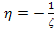
|