Self Consistent Method
The self consistent method is based on the solution to an auxiliary inclusion problem where a single ellipsoidal inclusion is embedded in an infinite medium. In this system it is assumed that the bond between inclusion and the infinite medium is perfect. Therefore, there is displacement and traction continuity across the interface of the two phases. One can determine the stresses and strains by applying uniform stresses or strains to the system at infinity. It was shown by Eshelby [1] that in these types of problems, the stress and strain fields in the inclusion are uniform. Further, the elastic properties can be determined by finding the relation between far-field stresses and strains in the homogeneous medium and stresses and strains in the inclusion, or the stress or strain concentration factors.
The problem of determining the effective properties of such a system was dealt in depth by Hill [2] and Budiansky [3]. In this approach the average stress and strain fields in the fiber are taken to be equal to those in the inclusion problem. Further, the infinite medium is taken to be homogeneous with the same properties of the composite.
For fibrous composites, which are transversely isotropic in nature with both fibre and matrix phases also transversely isotropic, the self consistent estimates of Hill [2] of the overall moduli give the following relations.
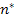 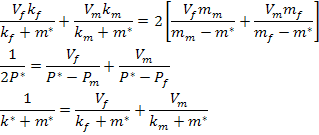 |
(7.283) |
It was shown by Hill [4] that regardless of the method used to obtain the estimates, only three of the five overall moduli of such composites are actually independent. Then the moduli 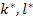 and and 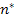 are related through so called universal relations in terms of overall moduli and phase moduli and their volume fractions as, are related through so called universal relations in terms of overall moduli and phase moduli and their volume fractions as,
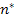 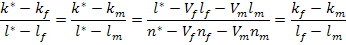 |
(7.284) |
Therefore, only one of the three moduli is independent. This fact is clear from the relation in Equation (7.283). This equation gives a cubic equation in 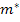 and quadratic equations for and quadratic equations for 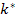 and and 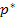 , again, in terms of , again, in terms of 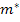 . Hence, if . Hence, if 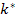 is known, then is known, then 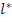 and and 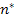 can easily be obtained from Eq. (7.284). can easily be obtained from Eq. (7.284).
Note: When one or both phases are isotropic, then there are only two independent moduli in such phase. Further, one can write then 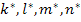 and and 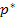 in terms of engineering constants. in terms of engineering constants.
|