The state of deformation imposed is such that the far away from the fibre and matrix a state of pure shear is produced.
The planar stresses for the cylinder can be given in terms of stress function 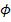 as as
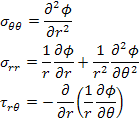 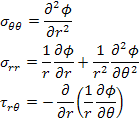 |
(7.254) |
where, the stress function 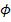 , following the work of [11], is given as , following the work of [11], is given as
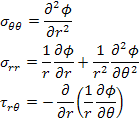 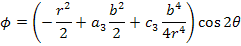 |
(7.255) |
Here, 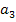 and and 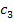 are the constants that are evaluated using the boundary conditions. Using Equation (7.255) in Equation (7.254), the stresses become are the constants that are evaluated using the boundary conditions. Using Equation (7.255) in Equation (7.254), the stresses become
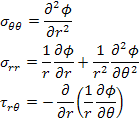 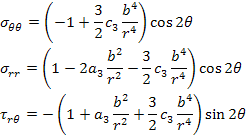 |
(7.256) |
Now, considering the plane strain condition with 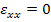 and using the stress-strain relations, the strains in composite material are written as and using the stress-strain relations, the strains in composite material are written as
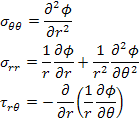 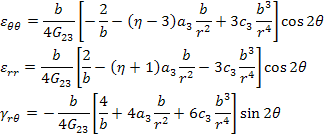 |
(7.257) |
where, 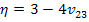 . Now using the strain displacement relations as in Equation (7.172) the displacement components in composite material are obtained as . Now using the strain displacement relations as in Equation (7.172) the displacement components in composite material are obtained as
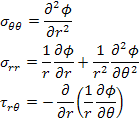 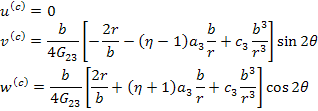 |
(7.258) |
Here, the polar coordinates are used. Further, as 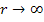 the above equation leads to the imposed state of simple shear deformation. It should be noted that the displacements in this equation satisfy the equilibrium equations. the above equation leads to the imposed state of simple shear deformation. It should be noted that the displacements in this equation satisfy the equilibrium equations.
|