Effective Axial Shear Modulus
The effective axial shear modulus is obtained by subjecting the concentric cylinders and equivalent homogeneous single cylinder to pure axial shear loading. Consider the concentric cylinders as shown in Figure 7.11. The outer surface of the cylinder in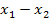 plane is subjected to a displacement field such that the overall strain produced in this plane is equal to plane is subjected to a displacement field such that the overall strain produced in this plane is equal to 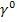 , that is, , that is,
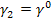 |
(7.240) |
The displacement components on the boundary of the cylinder then becomes
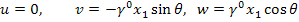 |
(7.241) |
Let us assume that both fibre and matrix materials are transversely isotropic in nature. Further, assume that they experience only shear strains. Under these assumptions, it can be shown that the each component of the displacement in either of the phase is governed by Laplace equation. For the details of the derivation one can see work by Chou and Pagano [7]. For the present case of deformations, the strains are not the function of 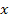 . The displacement components in each constituent are then given with corresponding simplification in the general solution as . The displacement components in each constituent are then given with corresponding simplification in the general solution as
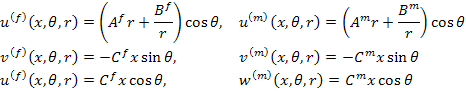 |
(7.242) |
|