It should be noted that the axisymmetric problem given here has the same form of solution as given previously. However, the constants involved in this problem will take different values depending upon the boundary conditions of this problem. For this problem in hand, we have the following boundary conditions:
The radial displacement at the fibre and matrix interface should be continuous as in the first of Equation (7.180).
The second condition is continuity of radial stresses at the fibre and matrix interface as in Equation (7.182). With transversely isotropic fibre, this condition leads to
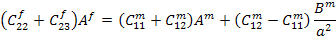 |
(7.224) |
and with isotropic fibre, this condition from Equation (7.202) with 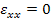 becomes becomes
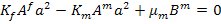 |
(7.225) |
The third condition is that the outer boundary of the cylinder has the radial stress equal to the 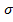 as in Equation (7.221) or Equation (7.222). In case of fibre with transversely isotropic material, this leads to as in Equation (7.221) or Equation (7.222). In case of fibre with transversely isotropic material, this leads to
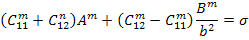 |
(7.226) |
and in case of fibre with isotropic material, from Equation (7.200) with 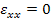 it becomes it becomes
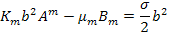 |
(7.227) |
For the case of transversely isotropic fibre the constants 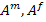 and and 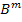 are determined by solving the Equations. (7.180), (7.224) and (7.226). These constants are are determined by solving the Equations. (7.180), (7.224) and (7.226). These constants are
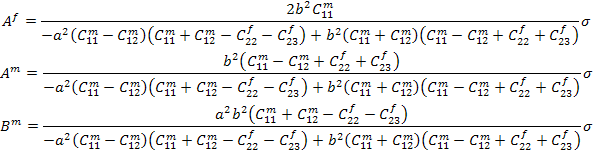 |
(7.228) |
For the case of isotropic fibre the the constants 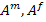 and and 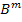 are determined by solving the Equations (7.180), (7.225) and (7.227). These constants are given as are determined by solving the Equations (7.180), (7.225) and (7.227). These constants are given as
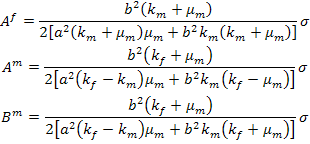 |
(7.229) |
Thus, all stresses and strains can be given in terms of unknown 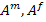 and and 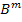 constants. The effective plane strain bulk modulus of the equivalent homogeneous material is then defined as constants. The effective plane strain bulk modulus of the equivalent homogeneous material is then defined as
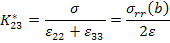 |
(7.230) |
From Equation (7.220), we can write
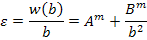 |
(7.231) |
Thus, combining Equation (7.230) and Equation (7.231) we get
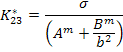 |
(7.232) |
The effective plane strain bulk modulus can be also defined as
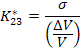 |
(7.233) |
where,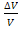 is the ratio of change in volume per unit volume of the concentric cylinders. It is given as is the ratio of change in volume per unit volume of the concentric cylinders. It is given as
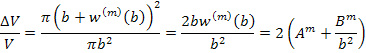 |
(7.234) |
In this the second order terms are ignored. Thus, the effective plane strain bulk modulus for this definition gives us same expression for plane strain bulk modulus as in Equation (7.232).
Thus, for the transversely isotropic fibre, using the constants as given in Equation (7.228) the effective plane strain bulk modulus becomes
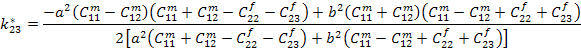 |
(7.235) |
Dividing the numerator and denominator by 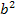 , we get , we get
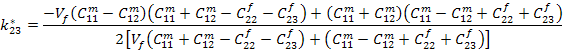 |
(7.236) |
For isotropic fibre, using the constants from Equation (7.229) the effective plane strain bulk modulus is given as
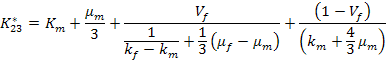 |
(7.237) |
|