Equivalence of Strain Energy Approach
In this approach the strain energies of the concentric cylinders and equivalent homogeneous cylinder are equated. The strain energy of the equivalent homogeneous cylinder is written as
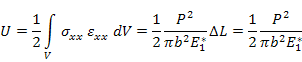 |
(7.211) |
In this equation a unit length of the cylinders has been assumed. Further, use of Equation (7.191) can be made in this equation. Now, the strain energy of the concentric cylinders is given as
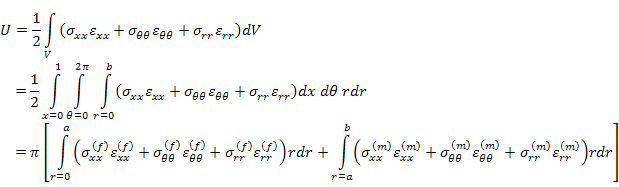 |
(7.212) |
Recall that the stresses are functions of 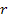 alone. They are independent of alone. They are independent of 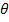 and and 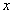 . Further, for this cylinder system also a unit length has been assumed. Equation (7.184) and Equation (7.185) are substituted in the above equation and integration over . Further, for this cylinder system also a unit length has been assumed. Equation (7.184) and Equation (7.185) are substituted in the above equation and integration over 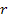 is carried out. It gives us is carried out. It gives us
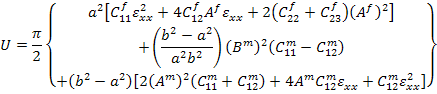 |
(7.213) |
Further, the unknown constants 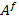 , ,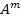 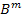 and and 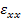 as given in Equation (7.192) are used. Then comparison of Equation (7.211) and Equation (7.213) gives the effective axial modulus as given in Equation (7.192) are used. Then comparison of Equation (7.211) and Equation (7.213) gives the effective axial modulus 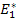 . .
Special Case: Fibre and Matrix Materials are Isotropic
The strain energy of the equivalent homogeneous cylinder obtained using Equation (7.211) and Equation (7.204). The strain energy of the concentric cylinders can be obtained using Equation (7.199) – Equation (7.201) and Equation (7.184) in the last of Equation (7.212). The strain energy for concentric cylinders is given as
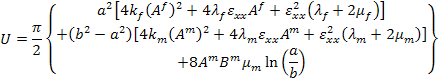 |
(7.214) |
In above equation, the unknown constants 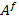 , ,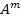 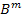 and and 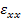 and as given Equation (7.205) can be used for further simplifications. Thus, equivalence of strain energies of concentric and equivalent homogeneous cylinder will lead to effective axial modulus and as given Equation (7.205) can be used for further simplifications. Thus, equivalence of strain energies of concentric and equivalent homogeneous cylinder will lead to effective axial modulus 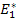 . .
|