|
Special Case: Fibre and Matrix Materials are Isotropic
The constitutive equations for an isotropic and linear elastic material, we write
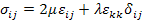 |
(7.198) |
where, 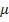 and and 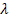 are the Lamé constants. Further, are the Lamé constants. Further, 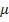 is shear modulus. To be consistent with the notations for shear modulus one can use the symbol is shear modulus. To be consistent with the notations for shear modulus one can use the symbol 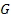 in the following derivations. However, we will use the symbol in the following derivations. However, we will use the symbol 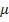 in this case. The axial stresses in fibre and matrix are given as in this case. The axial stresses in fibre and matrix are given as
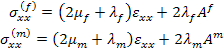 |
(7.199) |
Here, 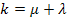 is defined as bulk modulus. The axial stress in fibre and matrix is spatially uniform. The radial stresses in fibre and matrix are given as is defined as bulk modulus. The axial stress in fibre and matrix is spatially uniform. The radial stresses in fibre and matrix are given as
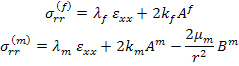 |
(7.200) |
The hoop stresses in fibre and matrix are
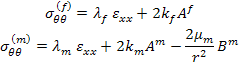 |
(7.201) |
These are the same as radial stresses. Further, as mentioned earlier all shear stresses are zero. |